Curve Fitting

Igor Pro's curve fitting capability is one of its strongest analysis features. Here are some of the highlights:

Linear and general nonlinear curve fitting.
Fit by ordinary least squares, or by least orthogonal distance for errors-in-variables models.
Fit to implicit models.
Built-in functions for common fits.
Automatic initial guesses for built-in functions.
Fitting to user-defined functions of any complexity.
Fitting to functions of any number of independent variables, either gridded data or multicolumn data.
Fitting to a sum of fit functions.
Fitting to a subset of a waveform or XY pair.
Produces estimates of error.
Supports weighting.

The idea of curve fitting is to find a mathematical model that fits your data. We assume that you have theoretical reasons for picking a function of a certain form. The curve fit finds the specific coefficients which make that function match your data as closely as possible.

You cannot use curve fitting to find which of thousands of functions fit a data set.

People also use curve fitting to merely show a smooth curve through their data. This sometimes works but you should also consider using smoothing or interpolation, which are described in Smoothing.

You can fit to three kinds of functions:

Built-in functions.
User-defined functions.
External functions (XFUNCs).

The built-in fitting functions are line, polynomial, sine, exponential, double-exponential, Gaussian, Lorentzian, Hill equation, sigmoid, lognormal, Gauss2D (two-dimensional Gaussian peak) and Poly2D (two-dimensional polynomial). See Built-in Curve Fitting Functions for more details about these functions.

You create a user-defined function by entering the function in the New Fit Function dialog. Very complicated functions may have to be entered in the Procedure window.

XFUNCs are written in C or C++. To create an XFUNC, you need the optional Igor XOP Toolkit and a C/C++ compiler. You don't need the toolkit to use an XFUNC that you get from WaveMetrics or from another user.

Curve fitting works with equations of the form y=f(x₁,x₂,...x_n); although you can fit functions of any number of independent variables (the x_n's) most cases involve just one. For more details on multivariate fitting, see Fitting to a Multivariate Function.

You can also fit to implicit functions; these have the form f(x₁,x₂,...x_n) = 0. See Fitting Implicit Functions.

You can do curve fits with linear constraints (see Fitting with Constraints).

Curve Fitting Terminology

Built-in fits are performed by the CurveFit operation. User-defined fits are performed by the FuncFit or FuncFitMD operation. We use the term "curve fit operation" below to stand for CurveFit, FuncFit, or FuncFitMD, whichever is appropriate.

Fitting to an external function works the same as fitting to a user-defined function (with some caveats concerning the Curve Fitting dialog — see Fitting to an External Function (XFUNC)).

If you use the Curve Fitting dialog, you don't really need to know much about the distinction between built-in and user-defined functions. You may need to know a bit about the distinction between external functions and other types. This will be discussed later.

We use the term "coefficients" for the numbers that the curve fit is to find. We use the term "parameters" to talk about the values that you pass to operations and functions.

Overview of Curve Fitting

In curve fitting we have raw data and a function with unknown coefficients. We want to find values for the coefficients such that the function matches the raw data as well as possible. The "best" values of the coefficients are the ones that minimize the value of Chi-square. Chi-square is defined as:

\displaystyle \sum_{i}\left(\frac{y-y_{i}}{\sigma_{i}}\right)^{2}

where y is a fitted value for a given point, y_i is the measured data value for the point and σ_i is an estimate of the standard deviation for y_i.

The simplest case is fitting to a straight line: y = ax + b. Suppose we have a theoretical reason to believe that our data should fall on a straight line. We want to find the coefficients a and b that best match our data.

For a straight line or polynomial function, we can find the best-fit coefficients in one step. This is noniterative curve fitting, which uses the singular value decomposition algorithm for polynomial fits.

Iterative Fitting

For the other built-in fitting functions and for user-defined functions, the operation is iterative as the fit tries various values for the unknown coefficients. For each try, it computes chi-square searching for the coefficient values that yield the minimum value of chi-square.

The Levenberg-Marquardt algorithm is used to search for the coefficient values that minimize chi-square. This is a form of nonlinear, least-squares fitting.

As the fit proceeds and better values are found, the chi-square value decreases. The fit is finished when the rate at which chi-square decreases is small enough.

During an iterative curve fit, you will see the Curve Fit progress window. This shows you the function being fit, the updated values of the coefficients , the value of chi-square, and the number of passes.

Normally you will let the fit proceed until completion when the Quit button is disabled and the OK button is enabled. When you click OK, the results of the fit are written in the history area.

If the fit has gone far enough and you are satisfied, you can click the Quit button, which finishes the iteration currently under way and then puts the results in the history area as if the fit had completed on its own.

Sometimes you can see that the fit is not working, e.g., when chi-square is not decreasing or when some of the coefficients oscillate in value. You can abort it by pressing the User Abort Key Combinations, which discards the results of the fit. You will need to adjust the fitting coefficients and try again.

Initial Guesses

The Levenberg-Marquardt algorithm is used to search for the minimum value of chi-square. Chi-square defines a surface in a multidimensional error space. The search process involves starting with an initial guess at the coefficient values. Starting from the initial guesses, the fit searches for the minimum value by travelling down hill from the starting point on the chi-square surface.

We want to find the deepest valley in the chi-square surface. This is a point on the surface where the coefficient values of the fitting function minimize, in the least-squares sense, the difference between the experimental data and fit data. Some fitting functions may have only one valley. In this case, when the bottom of the valley is found, the best fit has been found. Some functions, however, may have multiple valleys, places where the fit is better than surrounding values, but it may not be the best fit possible.

When the fit finds the bottom of a valley it concludes that the fit is complete even though there may be a deeper valley elsewhere on the surface. Which valley is found first depends on the initial guesses.

For built-in fitting functions, you can automatically set the initial guesses. If this produces unsatisfactory results, you can try manual guesses. For fitting to user-defined functions you must supply manual guesses.

Termination Criteria

A curve fit will terminate after 40 passes in searching for the best fit, but will quit if 9 passes in a row produce no decrease in chi-square. This can happen if the initial guesses are so good that the fit starts at the minimum chi-square. It can also happen if the initial guesses are way off or if the function does not fit the data at all.

You can change the 40-pass limit. See the discussion of V_FitMaxIters under Special Variables for Curve Fitting. Usually needing more than 40 passes is a sign of trouble with the fit. See Identifiability Problems.

Unless you know a great deal about the fitting function and the data, it is unwise to assume that a solution is a good one. In almost all cases you will want to see a graph of the solution to compare the solution with the data. You may also want to look at a graph of the residuals, the differences between the fitted model and the data. Igor makes it easy to do both in most cases.

Errors in Curve Fitting

In certain cases you may encounter a situation in which it is not possible to decide where to go next in searching for the minimum chi-square. This results in a "singular matrix" error. This is discussed under Singularities in Curve Fitting. Curve Fitting Troubleshooting can help you find the solution to the problem.

Data for Curve Fitting

You must have measured values of both the dependent variable (usually called "y") and the independent variables (usually called "x" especially if there is just one). These are sometimes called the "response variable" and "explanatory variables." You can do a curve fit to waveform data or to XY data. That is, you can fit data contained in a single wave, with the data values in the wave representing the Y data and the wave's X scaling representing equally-spaced X data. Or you can fit data from two (or more) waves in which the data values in one wave represent the Y values and the data values in another wave represent the X data. In this case, the data do not need to be equally spaced. In fact, the X data can be in random order.

You can read more about waveform and XY data under Waves.

The Quick Fit menu is the easiest, fastest way to do a curve fit:

The Quick Fit menu gives you quick access to curve fits using the built-in fitting functions. The data to be fit are determined by examining the top graph; if a single trace is found, the graphed data is fit to the selected fitting function. If the graph contains more than one trace a dialog is presented to allow you to select which trace should be fit.

The graph contextual menu also gives access to the Quick Fit menu. If you right-click on a trace in a graph, you will see a Quick Fit item at the bottom of the resulting contextual menu. When you access the Quick Fit menu this way, it automatically fits to the trace you clicked on. This gives you a way to avoid the dialog that Quick Fit uses to select the correct trace when there is more than one trace on a graph.

When you use the Quick Fit menu, a command is generated to perform the fit and automatically add the model curve to the graph. By default, if the graph cursors are present, only the data between the cursors is fit. You can do the fit to the entire data set by selecting the Fit Between Cursors item in the Quick Fit menu in order to uncheck the item. When unchecked, fits are done disregarding the graph cursors.

If the trace you are fitting has error bars, and the data for the error bars come from a wave, Quick Fit will use the wave as a weighting wave for the fit. Note that this assumes that your error bars represent one standard deviation. If your error wave represents more than one standard deviation, or if it represents a confidence interval, you should not use it for weighting. You can select the Weight from Error Bar Wave item to un-mark it, preventing Igor from using the error bar wave for weighting.

By default, a report of curve fit results is printed to the history. If you select Textbox Preferences, the Curve Fit Textbox Preferences dialog is displayed. It allows you to specify that a textbox be added to your graph containing most of the information that is printed in the history. You can select various components of the information by selecting items in the Dialog.

In the screen capture above, the poly2D and Gauss2D fit functions are not available because the top graph does not contain a contour plot or image plot, in which case the fitting functions would be available.

For a discussion of the built-in fit functions, see Built-in Curve Fitting Functions.

The Quick Fit menu does not give you access to the full range of curve fitting options available to you. It does not give you access to user-defined fitting functions, automatic residual calculation, masking, or confidence interval analysis. A Quick Fit always uses automatic guesses; if the automatic guesses don't work, you must use the Curve Fitting dialog to enter manual guesses.

If your graph displays an image that uses auxiliary X and Y waves to set the image pixel sizes, Quick Fit will not be able to do the fit. This is because these waves for an image plot have an extra point that makes them unsuitable for fitting. A contour plot uses X and Y waves that set the centers of the data, and these can be used for fitting. Quick Fit will do the right thing with such a contour plot.

Curve Fitting Using the Curve Fitting Dialog

If you want options that are not available via the Quick Fit menu, the next easiest way to do a fit is to choose Curve Fitting from the Analysis menu. This displays the Curve Fitting dialog, which presents an interface for selecting a fitting function and data waves, and for setting various curve fitting options. You can use the dialog to enter initial guesses if necessary. The Curve Fitting dialog can also be used to create a new user-defined fitting function.

Most curve fits can be accomplished using the Curve Fitting dialog. If you need to do many fits using the same fit function fitting to numerous data sets you will probably want to write a procedure in Igor's programming language to do the job.

The facility for creating a user-defined fitting function using the Curve Fitting dialog will handle most common cases, but is probably not the best way to create a very complex fitting function. In such cases, you will need to write a fitting function in a procedure window. This is described later under User-Defined Fitting Functions.

Some very complicated user-defined fitting functions may not work well with the Curve Fitting dialog. In some cases, you may need to write the fitting function in the Procedure window, and then use the dialog to set up and execute the fit. In other cases it may be necessary to enter the operation manually using either a user procedure or by typing on the command line. These cases should be quite rare.

A Simple Case -- Fitting to a Built-in Function: Line Fit

To get started, we will cover fitting to a simple built-in function: a line fit. You may have a theoretical reason to believe that your data should be described by the function y = ax + b. You may simply have an empirical observation that the data appear to fall along a line and you now want to characterize this line. It's better if you have a theoretical justification, but we're not all that lucky.

The Curve Fitting dialog is organized into four tabs. Each tab contains controls for some aspect of the operation. Simple fits to built-in functions using default options will require only the Function and Data tab.

We will go through the steps necessary to fit a line to data displayed in a graph. Other built-in functions work much the same way.

You might have data displayed in a graph like this:

Now you wish to find the best-fitting line for this data. The following commands will make a graph like this one. The SetRandomSeed command is used so that the "random" scatter produced by the enoise function will be the same as shown above. If you would like to perform the actions yourself, you can make the data shown here and the graph by typing these commands on the command line. You can execute commands in this help file by selecting the command lines by pressing Ctrl and Enter:

Make/N=20/D LineYData, LineXData
SetRandomSeed 0.5                   // So the example always makes the same "random" numbers
LineXData = enoise(2)+2             // enoise makes "random" numbers
LineYData = LineXData*3+gnoise(1)   // so does gnoise
Display LineYData vs LineXData
ModifyGraph mode=3,marker=8

The first line makes two waves to receive our "data". The second line sets the seed for Igor's pseudo-random number generators, resulting in reproducible noise. The third line fills the X wave with uniformly-distributed random numbers in the range of zero to four. The fourth line fills the Y wave with data that falls on a line having a slope of three and passing through the origin, with some normally-distributed noise added. The final two lines make the graph and set the display to markers mode with open circles as the marker.

Choosing the Function and Data

You display the Curve Fitting dialog by selecting Curve Fitting from the Analysis menu. If you have not used the dialog yet, it looks like this, with the Function and Data tab showing:

The first step in doing a curve fit is to select a fit function. We are doing a simple line fit, so pop up the Function menu and select "line":

Select the Y data from the Y Data menu. If you have waveform data, be sure that the X data menu has "_Calculated_" selected.

If you have separate X and Y data waves, you must select the X wave in the X Data menu. Only waves having the same number of data points as the Y wave are shown in this menu. A mismatch in the number of points is usually the problem if you don't see your X wave in the menu.

For the line fit example, we select LineYData from the Y Data menu, and LineXData from the X Data menu:

If you have a large number of waves in your experiment, it may be easier if you select the From Target checkbox. When it is selected only waves from the top graph or table are shown in the Y and X wave menus, and an attempt is made to select wave pairs used by a trace on the graph.

At this point, everything is set up to do the fit. For this simple case it is not necessary to visit the other tabs in the dialog. When you click Do It, the fit proceeds. The line fit example graph winds up looking like this:

In addition to the model line shown on the graph, various kinds of information appears in the history area:

•CurveFit line LineYData /X=LineXData /D
  fit_LineYData= W_coef[0]+W_coef[1]*x
  W_coef={-0.037971,2.9298}
  V_chisq= 18.25; V_npnts= 20; V_numNaNs= 0; V_numINFs= 0;
  V_startRow= 0;V_endRow= 19;V_q= 1;V_Rab= -0.879789;
  V_Pr= 0.956769;V_r2= 0.915408;
  W_sigma={0.474,0.21}
  Coefficient values ± one standard deviation
   a	=-0.037971 ± 0.474
   b	=2.9298 ± 0.21

Two Useful Additions: Holding a Coefficient and Generating Residuals

Well, you've done the fit and looked at the graph and you decide that you have reason to believe that the line should go through the origin. Because of the scatter in the measured Y values, the fit line misses the origin. The solution is to do the fit again, but with the Y intercept coefficient held at a value of zero.

You might also want to display the residuals as a visual check of the fit.

Bring up the dialog again. The dialog remembers the settings you used last time, so the line fit function is already selected on the Function menu, and your data waves are selected on the Y Data and X Data menus.

Select the Coefficients tab. Each of the coefficients has a row in the Coefficients list:

Click the checkbox in the column labeled "Hold?" to hold the value of the corresponding coefficient.

To specify a coefficient value, fill in the corresponding box in the Initial Guess column. Until you select the Hold box the initial guess box is not available because built-in fits don't require initial guesses.

To fill in a value, click in the box. You can now type a value. When you have finished, press Enter to exit editing mode for that box.

Now we want to calculate the fit residuals and add them to the graph. Click the Output Options tab and select _auto trace_ from the Residual menu:

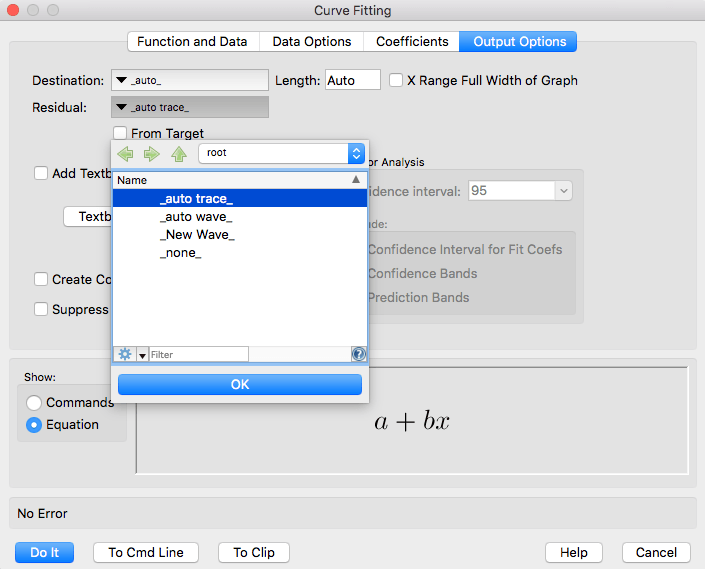
There are a number of options for the residual. We selected _auto trace_ to calculate the residual and add it to the graph. You may not always want the residuals added to your graph; select _auto wave_ to automatically calculate the residuals but not display them on your graph. Both _auto trace_ and _auto wave_ create a wave with the same name as your Y wave with "Res_" prefixed to the name. Selecting _New Wave_ generates commands to make a new wave with your choice of name to fill with residuals. It is not added to your graph.

Now when we click Do It, the fit is recalculated with a held at zero so that the line passes through the origin. Residuals are calculated and added to the graph:

Note that the line on the graph doesn't cross the vertical axis at zero, because the horizontal axis doesn't extend to zero.

Holding a at zero, the result of the fit printed in the history is:

•K0 = 0;
•CurveFit/H="10" line LineYData /X=LineXData /D /R
  fit_LineYData= W_coef[0]+W_coef[1]*x
  Res_LineYData= LineYData[p] - (W_coef[0]+W_coef[1]*LineXData[p])
  W_coef={0,2.915}
  V_chisq= 18.2565; V_npnts= 20; V_numNaNs= 0; V_numINFs= 0;
  V_startRow= 0; V_endRow= 19; V_q= 1; V_Rab= 0; V_Pr= 0.956769;
  V_r2= 0.906186;
  W_sigma={0,0.0971}
  Coefficient values ± one standard deviation
   a	=	0 ± 0
   b	=	2.915 ± 0.0971

The Automatic Guesses Didn't Work

Most built-in fits will work just like the line fit. You simply choose a function from the Function menu, choose your data wave (or waves if you have both X and Y waves) and select output options on the Output Options tab. For built-in fits you don't need the Coefficients tab unless you want to hold a coefficient.

In a few cases, however, automatic guesses don't work. Then you must use the Coefficient tab to set your own initial guesses. One important case in which this is true is if you are trying to fit a growing exponential, y = ae^bx, where b is positive.

Here are commands to create an example for this section. Once again, you can select the commands and execute them by typing Ctrl-Enter:

Make/N=20 RisingExponential
SetScale/I x 0,1,RisingExponential
SetRandomSeed 0.5
RisingExponential = 2*exp(3*x)+gnoise(1)
Display RisingExponential
ModifyGraph mode=3,marker=8

These commands make a 20-point wave, set its X scaling to cover the range from 0 to 1, fill it with exponential values plus a bit of noise, and make a graph:

The first-cut trial to fitting an exponential function is to select exp from the Function menu and the RisingExponential wave in the Y Data menu (if you are continuing from the previous section, you may need to go to the Coefficients tab and un-hold the y0 coefficient, and to the Output Options tab and de-select _auto trace_ in the Residual menu). Automatic guesses assume that the exponential is well described by a negative coefficient in the exponential, so the fit doesn't work:

•CurveFit exp RisingExponential /D
  Fit converged properly
  fit_RisingExponential= W_coef[0]+W_coef[1]*exp(-W_coef[2]*x)
  W_coef={108.87,-113.32,0.32737}
  V_chisq= 423.845;V_npnts= 20;V_numNaNs= 0;V_numINFs= 0;
  V_startRow= 0;V_endRow= 19;
  W_sigma={255,252,0.863}
  Coefficient values ± one standard deviation
  	y0    	=108.87 ± 255
  	A     	=-113.32 ± 252
  	invTau	=0.32737 ± 0.863

In addition to the fact that the graphed fit curve doesn't follow the data points, the estimated uncertainty for the fit coefficients is unreasonably large.

The solution is to provide your own initial guesses. Click the Coefficients tab and select Manual Guesses in the menu in the upper-right.

The Initial Guesses column in the Coefficients list is now available for you to type your own initial guesses, including a negative value for invTau. In this case, we might enter these initial guesses:

y0       0
A        2
invTau   -3

In response, Igor generates some extra commands for setting the initial guesses and this time the fit works correctly:

•K0 = 0; K1 = 2; K2 = -3;
•CurveFit/G exp RisingExponential /D
  Fit converged properly
  fit_RisingExponential= W_coef[0]+W_coef[1]*exp(-W_coef[2]*x)
  W_coef={-0.81174,2.2996,-2.8742}
  V_chisq= 15.6292;V_npnts= 20;V_numNaNs= 0;V_numINFs= 0;
  V_startRow= 0;V_endRow= 19;
  W_sigma={0.798,0.41,0.171}
  Coefficient values ± one standard deviation
	y0    	=-0.81174 ± 0.798
	A     	=2.2996 ± 0.41
	invTau	=-2.8742 ± 0.171

It may well be that finding a set of initial guesses from scratch is difficult. Automatic guesses might be a good starting point which will provide adequate initial guesses when modified. For this the dialog provides the Only Guess mode.

When Only Guess is selected, click Do It to create the automatic initial guesses, and then stop without trying to do the fit. Now, when you bring up the Curve Fitting dialog again, you can select the coefficient wave created by the auto guess (W_coef if you chose _default_ in the Coefficient Wave menu). Choosing this wave will set the initial guesses to the automatic guess values. Now select Manual Guesses and modify the initial guesses. The Graph Now button may help you find good initial guesses (see under The Coefficients Tab for a User-Defined Function).

Fits with Constants

A few of the built-in fit functions include constants that are not varied during the fit. They enter only to provide, for instance, a constant X offset to improve numerical stability. One such built-in fit function is the exp_XOffset fit function. It fits this equation:

\displaystyle y_{0}+A \exp \left(\frac{x-x_{0}}{\tau}\right)

Here, y₀, A and tau are fit coefficients - they are varied during iterative fitting, and their final values are the solution to the fit. On the other hand, x₀ is a constant - it is not varied, rather you give it any value you wish as part of the fit setup. In the case of the exp_XOffset fit function, if you do not set it yourself, it will be set by default to the minimum X value in your input data. For fits to data far from the origin, this improves numerical stability. Naturally, it affects the value of A in the final solution.

In the Curve Fitting dialog, when you select a built-in fit function that uses a constant, an additional edit box appears below the fit function menu where you can set the value of the constant. Setting it to the default value Auto causes Igor to set the constant to some reasonable value based on your input data.

When you do a fit using a built-in fit function that uses a constant, the output includes the wave W_fitConstants. Each element of this wave holds the value of one constant for the equation. At present, the wave will have just one element because there are no built-in fit functions that use more than one constant.

See Built-in Curve Fitting Functions for details on the constants used with specific fit functions.

Fitting to a User-Defined Function

Fitting to a user-defined function is much like fitting to a built-in function, with two main differences:

You must define the fitting function.
You must supply initial guesses.

To illustrate the creation of a user-defined fit function, we will create a function to fit a log function: y = C₁ + C₂ ln(x).

Creating the Function

To create a user-defined fitting function, click the New Fit Function button in the Function and Data tab of the Curve Fitting Dialog. The New Fit Function dialog is displayed:

You must fill in a name for your function, fill in the Fit Coefficients list with names for the coefficients, fill in the Independent Variables list with names for independent variables, and then enter a fit expression in the Fit Expression window.

The function name must conform to nonliberal naming rules. That means it must start with a letter, contain only letters, numbers or underscore characters, and it must be 255 or fewer bytes in length (see Object Names). It must not be the same as the name of another object like a built-in function, user procedure, or wave name.

For the example log function, we enter "LogFit":

Press Tab to move to the first entry in the Fit Coefficient list. There is always one blank entry in the list where you can add a new coefficient name; since we haven't entered anything yet, there is only one blank entry.

Each time you enter a name, press Enter. Igor accepts that name and makes a new blank entry where you can enter the next name. We enter C1 and C2 as the names:

Click in the first blank entry in the Independent Variables list. Most fit functions will require just a single independent variable. We choose to name our independent variable x:

It is now time to enter the fit expression. You will notice that when you have entered a name in the Independent Variables list, some text is entered in the expression window. The return value of the fit function (the Y value in most cases) is marked with something like "f(x) = ". If you had entered "temperature" as the independent variable, it would say "f(temperature) = ".

This "f() = " text is required; otherwise the return value of the function will be unknown.

The fit expression is not an algebraic expression. It must be entered in the same form as a command on the command line. If you need help constructing a legal expression, you may wish to read Assignment Statements. The expression you need to type is simply the right-hand side of an assignment statement. The log expression in our example will look like this:

Note that multiplication requires an explicit *.

The dialog will check the fit expression for simple errors. For instance, it will not make the Save Fit Function Now button available if any of the coefficients or independent variables are missing from the expression.

The dialog cannot check for correct expression syntax. If all the easily-checked items are correct, the Save Fit Function Now and Test Compile buttons are made available. Clicking either of them will enter a new function in the Procedure window and attempt to compile procedures. If you click the Save Fit Function Now button and compilation is successful, you are returned to the Curve Fitting dialog with the new function selected in the Function menu.

If compile errors occur, the compiler's error message is displayed in the status box, and the offending part of your expression is highlighted. A common error might be to misspell a coefficient name somewhere in your expression. For instance, if you had typed CC1 instead of C1 somewhere you might see something like this:

Note that C1 appears in the expression. Otherwise, the dialog would tell you that C1 is missing.

When everything is ready to go, click the Save Fit Function Now button to construct a function in the Procedure window. It includes comments in the function code that tell the dialog various kinds of information. Our example function looks like this:

Function LogFit(w,x) : FitFunc
	WAVE w
	Variable x

	//CurveFitDialog/ These comments were created by the Curve Fitting dialog. Altering them will
	//CurveFitDialog/ make the function less convenient to work with in the Curve Fitting dialog.
	//CurveFitDialog/ Equation:
	//CurveFitDialog/ f(x) = C1+C2*log(x)
	//CurveFitDialog/ End of Equation
	//CurveFitDialog/ Independent Variables 1
	//CurveFitDialog/ x
	//CurveFitDialog/ Coefficients 2
	//CurveFitDialog/ w[0] = C1
	//CurveFitDialog/ w[1] = C2

	return w[0]+w[1]*log(x)
End

You shouldn't have to deal with the code in the Procedure window unless your function is so complex that the dialog simply can't handle it. You can look at User-Defined Fitting Functions for details on how to write a fitting function in the Procedure window.

Having entered the fit expression correctly, click the Save Fit Function Now button, which returns you to the main Curve Fitting dialog. The Function menu will now have LogFit selected as the fitting function.

The Coefficients Tab for a User-Defined Function

To fit a user-defined function, you will need to enter initial guesses in the Coefficients tab.

Having created a user-defined fitting function (or simply having selected a preexisting one) you will find that the error message window at the bottom of the dialog now states, "You have selected a user-defined fit function so you must enter an initial guess for every fit coefficient. Go to the Coefficients Tab to do this."

When you have selected a user-defined fitting function, the Initial Guess column of the Coefficients List is available. You must enter a number in each row. Some functions may be difficult to fit; in such a case the initial guess may have to be pretty close to the final solution.

To help you find good initial guesses, the Coefficients tab includes the Graph Now button. This button will add a trace to the top graph showing your fitting function using the initial guesses you have entered. For instance:

You can change the values in the initial guess column and click the Graph Now button as many times as you wish. The trace will be updated with the changes each time.

The Graph Now button works as describe in The Destination Wave, with one exception: if you selected _none_ in the Destination pop-up menu of the Output Options tab, the Graph Now button works as if you selected _auto_. The Graph Now button honors your choices for destination wave style, and it makes a new wave if you selected _New Wave_. Unless you change the destination wave settings before clicking Do It, the wave set by Graph Now will be overwritten by the fit.

On the Coefficients tab you have the option of selecting an "epsilon" wave. An epsilon wave contains one epsilon value for each point in your coefficients wave. By default the Epsilon menu is set to _none_ indicating that the epsilon values are set to the default values.

Each epsilon value is used to calculate partial derivatives with respect to the fit coefficients. The partial derivatives are used to determine the search direction for the coefficients that give the smallest chi-square.

In most cases the epsilon values are not critical. However, you can supply your own if you have reason to believe that the default epsilon values are not providing acceptable partial derivatives (sometimes a singular matrix error can be avoided by using custom epsilon values). To specify epsilon values, either select a pre-existing wave from the Epsilon Wave menu, or select _New Wave_. Only waves having a number of points equal to the number of fit coefficients are shown in the menu. Either choice causes the Epsilon column to be shown in the Coefficients list, where you can enter values for epsilon.

If you select a wave from the Epsilon menu, the values in that wave are entered in the list. If you select _New Wave_, the dialog generates commands to create an epsilon wave and fill it with the values in the Epsilon column.

For more information about the epsilon wave and what it does, see The Epsilon Wave.

Making a User-Defined Function Always Available

Note that, because the fitting function is created in the Procedure window, it is stored as part of the experiment file. That means that it will be available for fitting while you are working on the experiment in which it was created, but will not be available when you work on other experiment files.

You can make the fit function available whenever you start up Igor Pro. Make a new procedure window using the Procedure item under New in the Windows menu. Find the fit function in the Procedure window, select all the text from Function through End and select Cut from the Edit menu. Paste the code into your new procedure window. Finally, select Save Procedure Window from the File menu and save in "Igor Pro User Files/Igor Procedures" (see Igor Pro User Files for details). The next time you start Igor Pro you will find that the function is available in all your experiments.

Removing a User-Defined Fitting Function

To remove a user-defined fitting function that you don't want any more, pull down the Windows menu and select Procedure Window. Find the function in the Procedure window (you can use Find from the Edit menu and search for the name of your function). Select all the text of the function definition from the word "Function" through the word "End" and delete the text.

If you have followed the directions in the section above for making the function always available, find the procedure file in "Igor Pro User Files/Igor Procedures", remove it from the folder, and then restart.

User-Defined fitting function Details

The New Fit Function dialog is the easiest way to enter a user-defined fit function. But if your fit expression is very long, or it requires multiple lines with local variables or conditionals, the dialog can be cumbersome. Certain special situations may call for a format that is not supported by the dialog.

For a complete discussion of user-defined fit function formats and the uses for different formats, see User-Defined Fitting Functions.

Fitting to an External Function (XFUNC)

An external function, or XFUNC, is a function provided via an Igor extension or plug-in. A programmer uses the XOP Toolkit to build an XFUNC. You don't need the toolkit to use one. An XFUNC must be installed before it can be used. See Igor Extensions.

An XFUNC can speed up curve fitting greatly if your fitting function requires a great deal of computation. The speed of fitting is usually dominated by other kinds of overhead and the effort of writing an XFUNC is not justified.

Fitting to an external function is just like fitting to a user-defined function, except that the Curve Fitting dialog has no way to find out how many fit coefficients are required. When you switch to the Coefficients tab, you will see an alert telling you of that fact. The solution to this problem is to select a coefficient wave with the correct number of points. You must create the wave before entering the Curve Fitting dialog.

When you select a coefficient wave the contents of the wave are used to build the Coefficients list. The wave values are entered in the Initial Guess column. If you change an initial guess, the dialog will generate the commands necessary to enter the new values in the wave.

The Coefficient Wave menu normally shows only those waves whose length is the same as the number of fit coefficients required by the fitting function. When you choose an XFUNC for fitting, the menu shows all waves. You have to know which one to select. We suggest using a wave name that tells you what the wave is for.

Igor doesn't know about coefficient names for an XFUNC. Coefficient names will be derived from the name of the coefficient wave you select. That is, if your coefficient wave is called "coefs", the coefficient names will be "coefs_0", "coefs_1", etc.

Of course, implementing your function in C or C++ is more time-consuming and requires both the XOP Toolkit from WaveMetrics, and a software development environment. See Igor Extensions for details on using the XOP Toolkit to create your own external function.

The Coefficient Wave

When you fit to a user-defined function, your initial guesses are transmitted to the curve fitting operation via a coefficient wave. The coefficients that result from the fit are output in a coefficient wave no matter what kind of function you select. For the most part, the Curve Fitting dialog hides this from you.

When you create a user-defined function, the dialog creates a function that takes a wave as the input containing the fit coefficients. But through special comments in the function code, the dialog gives names to each of the coefficients. A built-in function has names for the coefficients stored internally. Using these names, the dialog is able to hide from you some of the complexities of using a coefficient wave.

In the history printout following a curve fit, the coefficient values are reported both in the form of a wave assignment using the actual coefficients wave, and as a list using the coefficient names. For instance, here is the printout from the example user-defined fit earlier (Fitting to a User-Defined Function):

•FuncFit LogFit W_coef logData /D
  Fit converged properly
  fit_logData= LogFit(W_coef,x)
  W_coef={1.0041,0.99922}
  V_chisq= 0.00282525; V_npnts= 30; V_numNaNs= 0; V_numINFs= 0;
  W_sigma={0.00491,0.00679}
  Coefficient values ± one standard deviation
   C1 = 1.0041  ± 0.491
   C2 = 0.99922 ± 0.679

The wave assignment version can be copied to the command line and executed, or it can be used as a command in a user procedure. The list version is easier to read.

You control how to handle the coefficients wave using the Coefficient Wave menu on the Coefficients tab. Here are the options.

Default

When _default_ is selected it creates a wave called W_coef. For built-in fits this wave is used only for output. For user-defined fits it is also input. The dialog generates commands to put your initial guesses into the wave before the fit starts.

Explicit Wave

The Coefficient Wave menu lists any wave whose length matches the number of fit coefficients. If you select one of these waves, it is used for input and output from any fit.

When you select a wave from the menu the data in the wave is used to fill in the Initial Guess column in the Coefficients list. This can be used as a convenient way to enter initial guesses. If you select an explicit wave and then edit the initial guesses, the dialog generates commands to change the values in the selected coefficient wave before the fit starts. To avoid altering the contents of the wave, after selecting a wave with the initial guesses you want, you can select _default_ or _New Wave_. The initial guesses will be put into the new or default coefficients wave.

New Wave

A variation on the explicit coefficients wave is _New Wave_. This works just like an explicit wave except that the dialog generates commands to make the wave before the fit starts, so you don't have to remember to make it before entering the dialog. The wave is filled in with the values from the Initial Guess column.

The _New Wave_ option is convenient if you are doing a number of fits and you want to save the fit coefficients from each fit. If you use _default_ the results of a fit will overwrite the results from any previous fit.

Errors

Estimates of fitting errors (the estimated standard deviation of the fit coefficients) are automatically stored a wave named W_sigma. There is no user choice about this.

The Destination Wave

When performing a curve fit, it will calculate the model curve corresponding to the fit coefficients. As with most results, the model curve is stored as an array of numbers in a wave. This wave is the "destination wave".

The main purpose of the destination wave is to show what the fit function looks like with various coefficients during the fit operation and with the final fit coefficients when the operation is finished. You can choose no destination wave, an explicit destination wave or you can use the auto-trace feature.

You select the destination wave option on the Output Options tab of the dialog. Here are the options.

No Destination

You would choose no destination wave if you don't want graphic feedback during the fitting process and you don't need to graphically compare your raw data to the fitting function. This might be the case if you are batch fitting a large number of data sets. Select _none_ in the Destination menu.

Auto-trace

In most cases, auto-trace is recommended. You select auto-trace by selecting _auto_ from the Destination menu. When you select this, it automatically creates a new wave, sets its X scaling appropriately, and appends it to the top graph if the Y data wave is displayed in it. The name of the new wave is generated by prepending "fit_" to the name of the Y data wave. If a wave of that name already exists, it is overwritten. If the name exceeds the 255 character maximum for a wave, the name is truncated.

The number of points in the destination wave depends on the number of independent variables. For the most common case of a univariate fit, the default is 200 points. The rest of this discussion assumes you are fitting univariate data.

If you want to fit more than one function to the same raw data using auto-trace, you should rename the auto-trace wave after the fit so that it will not be overwritten by a subsequent fit. You can rename it using the Rename item in the Data menu or by executing a Rename command directly from the command line. You may also want to save the W_coef and W_sigma waves using the same technique.

Usually the auto-trace wave is set up as a waveform even if you are fitting to XY data. The X scaling of the auto-trace wave is set to spread the 200 points evenly over the X range of the raw data. When preferences are on, the auto-trace wave appended to the graph has the preferred line style (color, size, etc.) except that the line mode is always set to "lines between points", which is best suited to showing the curve fitting results.

Evenly-spaced data are not well suited to displaying a curve on a logarithmic axis. If your data are displayed using a log axis, the fit will create an XY pair of waves. The X wave will be named by prepending "fitX_" to the name of the Y data wave. This X wave is filled with exponentially-spaced X values spread out over the X range of the fit data. Of course, if you subsequently change the axis to a linear axis, the point spacing will not look right.

With _auto_ selected in the Destination menu, the dialog displays a box labelled Length. Use this to change the number of points in the destination wave. You can set this to any number greater than 3. The more points, the smoother the curve (up to a point). More points will also take longer to draw so the fit will be slower.

Explicit Destination

You can specify an explicit destination wave rather than using auto-trace. Use this if you want a model value at the X location of each of your input data points.

An explicit destination wave must have the same number of points as the Y data wave, so you should create it using the Duplicate operation. The Destination menu shows only waves that have the same number of points as the selected Y Data wave.

The explicit destination wave is not automatically appended to the top graph. Therefore, before executing the curve fit operation, you would normally execute commands like:

Duplicate/O yData, yDataFit
AppendToGraph yDataFit vs xData

If you are fitting waveform data rather than XY data, you would omit "vs xData" from the AppendToGraph command.

New Wave

As a convenience, the Curve Fitting dialog can create a destination wave for you if you select _New Wave_ from the Destination menu. It does this by generating a Duplicate command to duplicate your Y data wave and then uses it just like any other explicit destination wave. The new wave is not automatically appended to your graph so you will have to do that yourself after the fit is completed.

Fitting a Subset of the Data

A common problem is that you don't want to include all of the points in your data set in a curve fit. There are two methods for restricting a fit to a subset of points. You will find these options on the Data Options tab of the Curve Fitting dialog.

Selecting a Range to Fit

You can select a contiguous range of points in the Range box. The values that you use to specify the range for a curve fit are in terms of point or row numbers of the Y data wave. Note that if you are fitting to an XY pair of waves and your X values are in random order, you will not be selecting a contiguous range as it appears on a graph.

To simplify selecting the range, you can use graph cursors to select the start and end of the range. To use cursors, display your raw data in a graph. Display the info panel in the graph by selecting ShowInfo from the Graph menu. Drag the cursors onto your raw data. Then use the "cursors" button in the Curve Fitting dialog to generate a command to fit the cursor range.

Here is what a graph might look like after a fit over a subrange of a data set:

In this example, we used auto-trace for the destination. Notice that the trace appears over the selected range only. If we want to show the destination over a wider range, we need to change the destination wave's X scaling. These commands change the destination wave to show more points over a wider range:

Redimension/N=500 fit_data			// change to 500 points
SetScale x 13, 20, fit_data		// set domain from 13 to 20
fit_data= W_coef[0]+W_coef[1]/((x-W_coef[2])^2+W_coef[3])

The last line was copied from the history area, where it was displayed after the fit.

This produces the following graph:

If you use an explicit destination wave rather than auto-trace, it is helpful to set the destination wave to blanks (NaN) before performing the fit. As the fit progresses, it will store new values only in the destination wave range that corresponds to the range being fit. Also, it stores into the destination wave only at points where the source wave is not NaN or INF. If you don't preset the destination wave to blanks, you will wind up with a combination of new and old data in the destination wave.

These commands illustrate presetting the destination wave and then performing a curve fit to a range of an XY pair.

Duplicate/O yData, yDataFit		// make destination
yDataFit = NaN						// preset to blank (NaN)
AppendToGraph yDataFit vs xData
CurveFit lor yData(xcsr(A),xcsr(B)) /D=yDataFit

Another way to make the fit curve cover a wider range is to select the checkbox labelled X Range Full Width of Graph. You will find the checkbox on the Output Options tab of the Curve Fitting dialog.

Using a Mask Wave

Sometimes the points you want to exclude are not contiguous. This might be the case if you are fitting to a data set with occasional bad points. Or, in spectroscopic data you may want to fit regions of baseline and exclude points that are part of a spectroscopic peak. You can achieve the desired result using a mask wave.

The mask wave must have the same number of points as the Y Data wave. You fill in the mask wave with a NaN (Not-a-Number, blank cell) or zero corresponding to data points to exclude and nonzero for data points you want to include. You must create the mask wave before bringing up the Curve Fitting dialog. You may want to edit the mask wave in a table.

Enter a NaN in a table by typing "NaN" and pressing Return or Enter. Having entered on NaN, you can copy it to the clipboard to paste into other cells.

You can also use a wave assignment on the command line. If your data set has a bad data point at point 4, a suitable command to set point four in the mask wave would be:

BadPointMask[4] = NaN

When you have a suitable mask wave, you select it from the Data Mask menu on the Data Options tab.

You can use a mask with NaN points to suppress display of the masked points in a graph if you select the mask wave as an f(z) wave in the Modify Trace Appearance dialog. You could also use the same wave with the ModifyGraph mask keyword.

Weighting

You may provide a weighting wave if you want to assign greater or lesser importance to certain data points. You would do so for one of two reasons:

To get a better, more accurate fit.
To get more accurate error estimates for the fit coefficients.

The weighting wave is used in the calculation of chi-square. chi-square is defined as

\displaystyle \sum_{i}\left(\frac{y-y_{i}}{w_{i}}\right)^{2}

where y is a fitted value for a given point, y_i is the original data value for the point and w_i is the standard error for the point. The weighting wave provides the w_i values. The values in the weighting wave can be either 1/σ_i or simply σ_i, where σ_i is the standard deviation for each data value. If necessary, Igor takes the inverse of the weighting value before using it to perform the weighting.

You specify the wave containing your weighting values by selecting it from the Weighting menu in the Data Options tab. In addition you must specify whether your wave has standard deviations or inverse standard deviations in it. You do this by selecting one of the buttons below the menu:

Standard Deviation
1/Standard Deviation

Usually you would use standard deviations. Inverse standard deviations are permitted for historical reasons.

There are several ways in which you might obtain values for σ_i. For example, you might have a priori knowledge about the measurement process. If your data points are average values derived from repeated measurements, then the appropriate weight value is the standard error. That is the standard deviation of the repeated measurements divided by N^1/2. This assumes that your measurement errors are normally distributed with zero mean.

If your data are the result of counting, such as a histogram or a multi-channel detector, the appropriate weighting is sqrt(Y). This formula, however, makes infinite weighting for zero values, which isn't correct and will cause those points to be eliminated from the fit. It is common to substitute a value of 1 for the weights for zero points.

You can use a value of zero to completely exclude a given point from the fit process, but it is better to use a data mask wave for this purpose.

If you do not provide a weighting wave, then unity weights are used in the fit and the covariance matrix is normalized based on the assumption that the fit function is a good description of the data. The reported errors for the coefficients are calculated as the square root of the diagonal elements of the covariance matrix and therefore the normalization process will provide valid error estimates only if all the data points have roughly equal errors and if the fit function is, in fact, appropriate to the data.

If you do provide a weighting wave then the covariance matrix is not normalized and the accuracy of the reported coefficient errors rests on the accuracy of your weighting values. For this reason you should not use arbitrary values for the weights.

Proportional Weighting

In some cases, it is desirable to use weighting but you know only proportional weights, not absolute measurement errors. In this case, you can use weighting and after the fit is done, calculate reduced chi-square. The reduced chi-square can be used to adjust the reported error estimates for the fit coefficients. When you do this, the resulting reduced chi-square cannot be used to test goodness of fit.

For example, a data set having Gaussian errors that are proportional to X:

Make data = exp(-x/10) + gnoise((x+1)/1000)
Display data

Prepare a weighting wave that has weights proportional to X, but are not equal to the true measurement errors:

Duplicate data, data_wt
data_wt = x+1		// Right proportionality with X, but 1000 times too big

The fit has pretty meaningless coefficient errors because the weights provided were proportional to the true measurement errors, but 1000 times too big:

CurveFit/NTHR=0 exp data /W=data_wt /I=1 /D 
Fit converged properly
fit_data= W_coef[0]+W_coef[1]*exp(-W_coef[2]*x)
W_coef={0.0044805,0.99578,0.10063}
V_chisq= 0.000117533;V_npnts= 128;V_numNaNs= 0;V_numINFs= 0;
V_startRow= 0;V_endRow= 127;
W_sigma={5.78,5.74,1.15}
Coefficient values ± one standard deviation
	y0    	=0.0044805 ± 5.78
	A     	=0.99578 ± 5.74
	invTau	=0.10063 ± 1.15

So now we compute reduced errors based on reduced chi-square:

Variable reducedChiSquare = V_chisq/(V_npnts - numpnts(W_coef))
Duplicate W_sigma, reducedSigma
reducedSigma = W_sigma*sqrt(reducedChiSquare)

The resulting errors are more reasonable:

Print reducedSigma
reducedSigma[0]= {0.00560293,0.0055649,0.00111907}

Note that, as with any non-linear fitting, Gaussian statistics like this are not really applicable. The results should be used with caution.

Fitting to a Multivariate Function

A multivariate function is a function having more than one independent variable. This might arise if you have measured data over some two-dimensional area. You might measure surface temperature at a variety of locations, resulting in temperature as a function of both X and Y. It might also arise if you are trying to find dependencies of a process output on the various inputs, perhaps initial concentrations of reagents, plus temperature and pressure. Such a case might have a large number of independent variables.

Fitting a multivariate function is pretty much like fitting to a function with a single independent variable. This discussion assumes that you have already read the instructions above for fitting a univariate function.

You can create a new multivariate user-defined function by clicking the New Fit Function button. In the Independent Variables list, you would enter more than one variable name. You can use as many independent variables as you wish (within generous limits set by the length of a line in the procedure window).

A univariate function usually is written as y = f (x), and the Curve Fitting dialog reflects this in using "Y Data" and "X Data" to label the menus where you select the input data.

Multivariate data isn't so convenient. Functions intended to fit spatial data are often written as z = f (x,y); volumetric data may be g= f (x,y,z). Functions of a large number of independent variables are often written as y = f (x₁,x₂, ...). To avoid confusion, we just keep the Y Data and X Data labels and use them to mean dependent variable and independent variables.

The principle difference between univariate and multivariate functions is in the selection of input data. If you have four or fewer independent variables, you can use a multidimensional wave to hold the Y values. This would be appropriate for data measured on a spatial grid, or any other data measured at regularly-spaced intervals in each of the independent variables. We refer to data in a multidimensional wave as "gridded data."

Alternately, you can use a 1D wave to hold the Y values. The independent variables can then be in N 1D waves, one wave for each independent variable, or a single N-column matrix wave. The X wave or waves must have the same number of rows as the Y wave.

Selecting a Multivariate Function

When the Curve Fitting dialog is first used, multivariate functions are not listed in the Function menu. The first thing you must do is to turn on the listing of multivariate functions. You do this by checking Show Multivariate Functions in the Function menu. This makes two built-in multivariate functions, poly2D and Gauss2D, as well as suitable user-defined functions, appear in the menu.

The Show Multivariate Functions setting is saved in the preferences. Unless you turn it off again, you never need select it again.

Now you can select your multivariate function from the menu.

Selecting Fit Data for a Multivariate Function

When you have selected a multivariate function, the Y Data menu is filled with 1D waves and any multidimensional waves that match the number of independent variables required by the fit function.

Selecting X Data for a 1D Y Data Wave

If your Y data are in a 1D wave, you must select an X wave for each independent variable. There is no way to store X scaling data in the Y wave for more than one independent variable, so there is no _calculated_ item.

With a 1D wave selected in the Y Data menu, the X Data menu lists both 1D waves and 2D waves with N columns for a function with N independent variables.

As you select X waves, the wave names are transferred to a list below the menu. When you have selected the right number of waves the X Data menu is disabled. The order in which you select the X waves is important. The first selected wave gives values for the first independent variable, etc.

If you need to remove an X Data wave from the list, simply click on the wave name and press Backspace. To change the order of X Data waves, select one or more waves in the list and drag them into the proper order.

Selecting X Data for Gridded Y Data

When you select a multidimensional Y wave, the independent variable values can come from the dimension scaling of the Y wave or from 1D waves containing values for the associated dimensions of the Y wave. That is, if you have a 2D matrix Y wave, you could select a wave to give values for the X dimension and a wave to give values for the Y dimension. The Independent Variable menus list only waves that match the given dimension of the Y wave.

Fitting a Subrange of the Data for a Multivariate Function

Selecting a subrange of data for a 1D Y wave is just like selecting a subrange for a univariate function. Simply enter point numbers in the Start and End range boxes in the Data Options tab.

If you are fitting gridded Y data, the Data Options tab displays eight boxes to set start and end ranges for each dimension of a multidimensional wave. Enter row, column, layer or chunk numbers in these boxes.

If your Y wave is a matrix wave displayed in a graph as an image, you can use the cursors to select a subset of the data. With the graph as the target window, clicking the Cursors button will enter text in the range boxes to do this.

Using cursors with a contour plot is not straightforward, and the dialog does not support it.

You can also select data subranges using a data mask wave (see Using a Mask Wave). The data mask wave must have the same number of points and dimensions as the Y Data wave.

Model Results for Multivariate Fitting

As with fitting to a function of one independent variable, Igor creates waves containing the model output and residuals automatically. This is done if you select _auto_ for the destination and _auto trace_ for the residual on the Output Options tab. There are some differences in detail, however.

By default, the model curve for a univariate fit is a smooth curve having 200 points to display the model fit. This depends on being able to sensibly interpolate between successive values of the independent variable. Multicolumn independent variables, on the other hand, probably don't have successive values of all the independent variables in sequential order, so it is not possible to do this. Consequently, it calculates a model point for each point in the dependent variable data wave. If the data wave is displayed as a simple 1D trace in the top graph window, the fit results will be appended to the graph.

Residuals are always calculated on a point-for-point basis, so calculating residuals for a multicolumn multivariate fit is just like a univariate fit.

Displaying results of fitting to a multidimensional wave is more problematic. If the dependent variable has three or more dimensions, it is not easy to display the results. The model and residual waves will be created and the results calculated but not displayed. You can make a variety of 3D plots using Gizmo: just choose the appropriate plot type from the Windows→New→3D Plots menu.

Fits to a 2D matrix wave are displayed on the top graph if the Y Data wave is displayed there as either an image or a contour. The model results are plotted as a contour regardless of whether the data are displayed as an image or a contour. Model results contoured on top of data displayed as an image can be a very powerful visualization technique.

Residuals are displayed in the same manner as the data in a separate, automatically-created graph window. The window size will be the same as the window displaying the data.

Time Required to Update the Display

Since contours and images can take quite a while to redraw, the time to update the display at every iteration may cause fits to contour or image data to be very slow. To suppress the updates, click the Suppress Screen Updates checkbox on the Output Options tab.

Multivariate Fitting Examples

Here are two examples of fitting to a multivariate function — the first uses the built-in poly2D function to fit a plane to a gridded dataset in order to remove a planar trend from the data. The second defines a simplified 2D gaussian function and uses it to define the location of a peak in XY space using random XYZ data.

Example One — Remove Planar Trend Using Poly2D

Here is an example in which a matrix is filled with a two-dimensional sinusoid with a planar trend that overwhelms the sinusoid. The example shows how you might fit a plane to the data in order to remove the trend. First, make the data matrix, fill it with values, and display the matrix as an image:

Make/O/N=(20,20) MatrixWave
SetScale/I x 0,2*pi,MatrixWave
SetScale/I y 0,2*pi,MatrixWave
MatrixWave = sin(x) + sin(y) + 5*x + 10*y
Display;AppendImage MatrixWave

These commands make a graph displaying an image like the one that follows. Note the gradient from the lower left to the upper right:

We are ready to do the fit.

Select Curve Fitting from the Analysis menu to bring up the Curve Fitting dialog.
If you have not already done so, select Show Multivariate Functions from the Function menu.
Select Poly2D from the Function menu.
Make sure the 2D Polynomial Order is set to 1.
Select MatrixWave from the Y Data menu.
Click on the Output Options tab.
Select _auto trace_ from the Residual menu.
Click Do It.

The result is the original graph with a contour plot showing the fit to the data, and a new graph of the residuals, showing the sinusoidal signal left over from the fit:

Similarly, you can use the ImageRemoveBackground operation, which provides a one-step operation to do the same fit. With an image plot as the top window, you will find Remove Background in the Image menu.

Example Two — User-Defined Simplified 2D Gaussian Fit

In this example, we have data defining a spot which we wish to fit with a 2D Gaussian in order to find the center of the spot. For some reason this data is in the form of XYZ triplets with random X and Y coordinates. These commands will generate the example data:

Make/N=300 SpotXData, SpotYData, SpotZData
SetRandomSeed 0.5
SpotXData = enoise(1)
SpotYData = enoise(1)
// make a gaussian centered at {0.55, -0.3}
SpotZData = 2*exp(-((SpotXData-.55)/.2)^2 -((SpotYData+.3)/.2)^2)+gnoise(.1)
Display; AppendXYZContour SpotZData vs {SpotXData,SpotYData}

Now bring up the Curve Fitting dialog and click the New Fit Function button so that you can enter your user-defined fit function. We have reason to believe that the spot is circular so the gaussian can use the same width in the X and Y directions, and there is no need for the cross-correlation term. Thus, the new function has a z0 coefficient for the baseline offset, A for amplitude, x0 and y0 for the X and Y location and w for width. Here is what it looks like in the New Fit Function dialog:

Click Save Fit Function Now to save the function in the Procedure window and return to the Curve Fitting dialog. The new function is selected in the Function menu automatically.

To perform the fit:

Select SpotZData in the Y Data menu.
Select SpotXData in the X Data menu.
Select SpotYData in the X Data menu.

At this point, the data selection area of the Function and Data tab looks like this:

Click the Coefficients tab (the error box at the bottom is telling us that we must enter initial guesses).
Enter initial guesses: we set z0 to 0, A to 2, x0 to 0.5, y0 to -0.3, and width to 0.5.
For our problem, residuals and destination aren't really important since we just want to know the coordinates of the spot center. We click Do It and get this in history:

FuncFit SimpleGaussian W_coef SpotZData /X={SpotXData,SpotYData} /D
  Fit converged properly
  fit_SpotZData= SimpleGaussian(W_coef,x,y)
  W_coef={1.9797,0.54673,-0.2977,0.19962,-0.0067009}
  V_chisq= 3.06428;V_npnts= 300;V_numNaNs= 0;V_numINFs= 0;
  V_startRow= 0;V_endRow= 299;
  W_sigma={0.065,0.00559,0.00553,0.00529,0.00622}
  Coefficient values ± one standard deviation
  	A 	=1.9797 ± 0.065
  	x0	=0.54673 ± 0.00559
  	y0	=-0.2977 ± 0.00553
  	w 	=0.19962 ± 0.00529
  	z0	=-0.0067009 ± 0.00622

The output shows that the fit has determined that the center of the spot is {0.54697, -0.30557}.

Problems with the Curve Fitting Dialog

Occasionally you may find that things don't work the way you expect when using the Curve Fitting dialog. Common problems are:

You can't find your user-defined function in the Function menu.

This usually happens for one of two reasons: either your function is a multivariate function or it is an old-style function. The problem is solved by selecting Show Multivariate Functions or Show Old-Style Functions from the Function menu on the Function and Data tab.

If you find that selecting Show Old-Style Functions makes your fit function appear, you may want to consider clicking on the Edit Fit Function button. This causes the Edit Fit Function dialog to appear. Part of the initialization for the dialog involves revising your fit function in order to make it conform to current standards. While you're there you can give your fit coefficients mnemonic names.
You get a message that "Igor can't determine the number of coefficients...".

This happens when you click on the Coefficients tab when you are using an external function or a user-defined function that is so complicated that the dialog can't parse the function code to determine how many coefficients are required.

The only way to get around this is to select an explicit coefficient wave (The Coefficient Wave). The dialog will then use the number of points in the coefficient wave to determine the number of coefficients.

Built-in Curve Fitting Functions

For the most part you will get good results using automatic guesses. A few require additional input beyond what is summarized in the preceding sections. This section contains notes on the fitting functions that give a bit more detail where it may be helpful.

gauss

Fits a Gaussian peak.


$\displaystyle y_{0}+A \exp \left[-\left(\frac{x-x_{0}}{\text { width }}\right)^{2}\right]$

Note that the width parameter is sqrt(2) times the standard deviation of the peak. This is different from the w_i parameter in the Gauss function, which is simply the standard deviation.

lor

Fits a Lorentzian peak.


$\displaystyle y_{0}+\frac{A}{\left(x-x_{0}\right)^{2}+B}$

Voigt

Fits a Voigt peak, a convolution of a Lorentzian and a Gaussian peak. By changing the ratio of the widths of the Lorentzian and Gaussian peak components the shape can grade between a Lorentzian shape and a Gaussian shape.

\displaystyle y_{0}+\frac{2 A r e a}{W_{G}} \sqrt{\frac{\ln (2)}{\pi}} \bullet \operatorname{Voigt}\left[\frac{2 \sqrt{\ln (2)}}{W_{G}}\left(x-x_{0}\right), \text { Shape } \bullet 2 \sqrt{\ln (2)}\right]

The Voigt function is a normalized Voigt peak shape function. It is the same as the built-in function VoigtFunc.

The premultiplier and arguments to the Voigt function result in a peak shape in which fit coefficients are:


Area	The area under the peak excluding the vertical offset
y0	The vertical offset
W_G	The Gaussian full width at half maximum (FWHM)
Shape	The ratio of the Lorentzian and Gaussian components, W_L/W_G

There is no analytic expression to compute the height of a Voigt peak.

The FWHM of the Voigt peak can be approximated as

\displaystyle W_{V}=\frac{W_{L}}{2}+\sqrt{\frac{W_{L}^{2}}{4}+W_{G}^{2}}

where W_L = Shape * W_G.

Fitting peaks with extreme values of Shape is not recommended as it suffers from numerical instability. Fit the end-point shapes Lor (Shape → ∞) or Gauss (Shape = 0) instead.

exp_XOffset

Fits a decaying exponential.


$\displaystyle y_{0}+A \exp \left\{\frac{-\left(x-x_{0}\right)}{\tau}\right\}$

In this equation, x₀ is a constant, not a fit coefficient. During generation of automatic guesses, x₀ will be set to the first X value in your fit data. This eliminates problems caused by floating-point roundoff.

You can set the value of x₀ using the /K flag with the CurveFit operation, but it is recommended that you accept the automatic value. Setting x₀ to a value far from the initial X value in your input data is guaranteed to cause problems.

note

The fit coefficient tau is the inverse of the equivalent coefficient in the exp function. It is actually the decay constant, not the inverse decay constant.

Automatic guesses don't work for growing exponentials (negative tau). To fit a negative value of tau, use Manual Guess on the Coefficients tab, or CurveFit/G on the command line.

dblexp_XOffset

Fits a sum of two decaying exponentials.


$\displaystyle y_{0}+A_{1} \exp \left\{\frac{-\left(x-x_{0}\right)}{\tau_{1}}\right\}+A_{2} \exp \left\{\frac{-\left(x-x_{0}\right)}{\tau_{2}}\right\}$

In this equation, x₀ is a constant, not a fit coefficient. During generation of automatic guesses, x₀ will be set to the smallest X value in your fit data. This eliminates problems caused by floating-point roundoff.

note

The fit coefficients tau₁ and tau₂ are the inverse of the equivalent coefficients in the dblexp function. They are actual decay constants, not inverse decay constants.

See the notes for exp_XOffset for growing exponentials. You will also need to use manual guesses if the amplitudes have opposite signs:

See also the dblexp_peak fit function described below.

If the two decay constants (tau₁ and tau₂) are not quite distinct you may not get accurate results.

exp

Fits a decaying exponential. Similar to exp_XOffset, but not as robust. Included for backward compatibility; in new work you should use exp_Xoffset.


$\displaystyle y_{0}+A \exp (-B x)$

Note that offsetting your data in the X direction will cause changes in A. Use exp_XOffset for a result that is independent of X position.

note

The fit coefficient B is the inverse decay constant.

Automatic guesses don't work for growing exponentials (negative B). To fit a negative value of B, use Manual Guess on the Coefficients tab, or CurveFit/G on the command line.

Floating-point arithmetic overflows will cause problems when fitting exponentials with large X offsets. This problem often arises when fitting decays in time as times are often large. The best solution is to use the exp_XOffset fit function. Otherwise, to fit such data, the X values must be offset back toward zero.

You could simply change your input X values, but it is usually best to work on a copy. Use the Duplicate command on the command line, or the Duplicate Waves item in the Data menu to copy your data.

For an XY pair, execute these commands on the command line (these commands assume that you have made a duplicate wave called myXWave_copy):

Variable xoffset = myXWave_copy[0]
myWave_copy[0] -= xoffset

Note that these commands assume that you are fitting data from the beginning of the wave. If you are fitting a subset, replace [0] with the point number of the first point you are fitting. If you are using graph cursors to select the points, substitute [pcsr(A)]. This assumes that the round cursor (cursor A) marks the beginning of the data.

If you are fitting to waveform data (you selected _calculated_ in the X Data menu) then you need to set the x0 part of the wave scaling to offset the data. If you are fitting the entire wave, simply use the Change Wave Scaling dialog from the Data menu to set the x0 part of the scaling to zero. If you are fitting a subset selected by graph cursors, it is easier to change the scaling on the command line:

SetScale/P x leftx(myWave_copy)-xcsr(A), deltax(myWave_copy), myWave_copy

This command assumes that you have used the round cursor (cursor A) to mark the beginning of the data.

Subtracting an X offset will change the amplitude coefficient in the fit. Often the only coefficient of interest is the decay constant (invTau) and the change in the amplitude can be ignored. If that is not the case, you can calculate the correct amplitude after the fit is done:

W_coef[1] = W_coef[1]*exp(W_coef[2]*xoffset)

If you are fitting waveform data, the value of xoffset would be -leftx(myWave_copy).

dblexp

Fits a sum of decaying exponentials. Similar to dblexp_XOffset, but suffers from floating-point roundoff problems if the data do not start quite close to x=0. Included for backward compatibility; in new work you should use exp_Xoffset.


$\displaystyle y_{0}+A_{1} \exp \left(-B_{1} x\right)+A_{2} \exp \left(-B_{2} x\right)$

Note that offsetting your data in the X direction will cause changes in A₁ and A₂. Use dblexp_XOffset for a result that is independent of X position.

note

The fit coefficients B₁ and B₂ are inverse decay constants.

See the notes for exp for growing exponentials. You will also need to use manual guesses if the amplitudes have opposite signs:

See also the dblexp_peak fit function described below.

If the two decay constants (B₁ and B₂ ) are not quite distinct you may not get accurate results.

Fitting data with a large X offset will have the same sort of troubles as when fitting with exp. The best solution is to use the dblexp_XOffset fit function; you can also solve the problem using a procedure similar to the one outlined for exp above.

dblexp_peak

Fits the sum of two exponential terms of opposite sign, making a peak.


$\displaystyle y_{0}+A \cdot\left\{-\exp \left[\frac{-\left(x-x_{0}\right)}{t a u_{1}}\right]+\exp \left[\frac{-\left(x-x_{0}\right)}{t a u_{2}}\right]\right\}$

The location of the peak is given by

X_{p e a k}=\frac{t a u_{1} t a u_{2} l n\left(\displaystyle \frac{t a u_{1}}{t a u_{2}}\right)}{t a u_{1}-t a u_{2}}+x_{0}

If you need individual control of the amplitudes of the two terms, use the dblexp_XOffset function. In that case, you will need to use manual guesses.

sin

Fits a sinusoid.


$\displaystyle \left(y_{0}+A \sin (f x+\phi)\right)$

phi is in radians. To convert to degrees, multiply by 180/Pi.

A sinusoidal fit takes an additional parameter that tells the auto guess the approximate frequency of the sinusoid. This is entered in terms of the approximate number of data points per cycle. When you select sin from the Function menu, a box appears where you enter the expected number of points per cycle.

If you enter a number less than 6, the default value is 7. It may be necessary to try various values to get good results. You may want to simply use manual guesses.

The nature of the sin function makes it impossible for a curve fit to distinguish phases that are different by 2π. It is probably easier to subtract 2nπ than to try to get the fit to fall in the desired range.

line

Fit a straight line through the data.


$\displaystyle (a+b x)$

Never requires manual guesses.

If you want to fit a line through the origin, in the Coefficients tab select the Hold box for coefficient a and set the Initial Guess value to zero.

poly n

Fits a polynomial with n terms, or order n-1.


$\displaystyle \left(K_{0}+K_{1} x+K_{2} x^{2}+\ldots\right)$

A polynomial fit takes an additional parameter that sets the number of polynomial terms. When you select poly from the Function menu, a box appears where you enter that value.

The minimum value of n is 1 corresponding to taking the mean of the Y value. Most Igor users won't need anything less than 3, a quadratic polynomial.

A polynomial fit never requires manual guesses.

poly_XOffset n

Fits a polynomial with n terms, or order n-1. The constant x₀ is not an adjustable fit coefficient; it allows you to place the polynomial anywhere along the X axis. This would be particularly useful for situations in which the X values are large, for instance when dealing with date/time data.


$\displaystyle \left(K_{0}+K_{1}\left(x-x_{0}\right)+K_{2}\left(x-x_{0}\right)^{2}+\ldots\right)$

The poly_XOffset fit function takes additional parameters that set the number of polynomial terms and the value of x₀. When you select poly_XOffset from the Function menu, boxes appear where you enter these values.

The minimum value of n is 1 corresponding to taking the mean of the Y value. Most Igor users won't need anything less than 3, a quadratic polynomial.

When Set Constant X0 is set to Auto, x₀ is set to the minimum X value found in the data you are fitting. You can set x₀ to any value you wish. Values far from the X values in your data set will cause numerical problems.

A polynomial fit never requires manual guesses.

Hill Equation

Fits Hill's Equation, a sigmoidal function.


$\displaystyle \text { base }+\frac{(\max -\text { base })}{1+\left(\frac{x_{1 / 2}}{x}\right)^{\text {rate }}}$

The coefficient base sets the y value at small X, max sets the y value at large X, rate sets the rise rate and x_1/2 sets the X value at which Y is at (base + max)/2.

Note that X values must be greater than 0. Including a data point at X<=0 will result in a singular matrix error and the message, "The fitting function returned NaN for at least one X value."

You can reverse the values of base and max to fit a falling sigmoid.

sigmoid

Fits a sigmoidal function with a different shape than Hill's equation.


$\displaystyle \text { base }+\frac{\max }{1+\exp \left(\frac{x_{0}-x}{\text { rate }}\right)}$

The coefficient base sets the Y value at small X. The Y value at large X is base + max. x₀ sets the X value at which Y is at (base + max/2) and rate sets the rise rate. Smaller rate causes a faster rise, specifically, the slope at x=x0 is max/(4 * rate).

power

Fits a power law.


$\displaystyle \left(y_{0}+A x^{pow}\right)$

May be difficult to fit, requiring good initial guesses, especially for pow > 1 or pow close to zero.

Note that X values must be greater than 0. Including a data point at X<=0 will result in a singular matrix error and the message, "The fitting function returned NaN for at least one X value."

lognormal

Fits a lognormal peak shape. This function is gaussian when plotted on a log X axis.


$\displaystyle y_{0}+A \exp \left[-\left(\frac{\ln \left(x / x_{0}\right)}{\text { width }}\right)^{2}\right]$

Coefficient y₀ sets the baseline, A sets the amplitude, x₀ sets the peak position in X and width sets the peak width.

Note that X values must be greater than 0. Including a data point at X<=0 will cause a singular matrix error and the message, "The fitting function returned NaN for at least one X value."

log

Fits a logarithmic curve.


$\displaystyle a+b \cdot \log _{10}(x)$

log is very forgiving of bad initial guesses. It was added in Igor Pro 9.00.

X values must be greater than 0. Including a data point with X<=0 results in a singular matrix error and the message "The fitting function returned NaN for at least one X value."

gauss2D

Fits a Gaussian peak in two dimensions.


$\displaystyle z_{0}+A \exp \left[\frac{-1}{2\left(1-{ cor }^{2}\right)}\left(\left(\frac{x-x_{0}}{{ xwidth }}\right)^{2}+\left(\frac{y-y_{0}}{{ ywidth }}\right)^{2}-\frac{2 {cor}\left(x-x_{0}\right)\left(y-y_{0}\right)}{{ xwidth } \cdot { ywidth }}\right)\right]$

Coefficient cor is the cross-correlation term; it must be between -1 and 1 (the small illustration was done with cor equal to 0.5). A constraint automatically enforces this range. If you know that a value of zero for this term is appropriate, you can hold this coefficient. Holding cor at zero usually speeds up the fit quite a bit.

In contrast with the gauss fit function, xWidth and yWidth are standard deviations of the peak.

Note that the Gauss function lacks the cross-correlation parameter cor.

poly2D n

Fits a polynomial of order n in two dimensions.


$\displaystyle \left(C_{0}+C_{1} x+C_{2} y+C_{3} x^{2}+C_{4} x y+C_{5} y^{2}+\ldots\right)$

A poly2D fit takes an additional parameter that tells the order of the polynomial. When you select poly2D from the Function menu, a box appears where you enter that value.

The minimum value is 1, corresponding to a first-order polynomial, a plane. The coefficient wave for poly2D has the constant term (K₀) in point zero, and following points contain groups of increasing order. There are two first-order terms, K₁*x and K₂*y, then three second-order terms, etc. The total number of terms is (N+1)(N+2)/2, where N is the order.

Poly2D never requires manual guesses.

Inputs and Outputs for Built-in Fits

There are a number of variables and waves that provide various kinds of input and output to a curve fit. Usually you will use the Curve Fitting dialog and the dialog will make it clear what you need, and detailed descriptions are available in various places in this help file. For a quick introduction, here is a table that lists the waves and variables used for fitting to a built-in function.

Wave or Variable	Type	What it is used for
Dependent variable data wave	Input	Contains measured values of the dependent variable of the curve to fit. Often referred to as "Y data".
Independent variable data wave	Input	Contains measured values of the independent variable of the curve to fit. Often referred to as "X data".
Destination wave	Optional output	For graphical feedback during and after the fit. The destination wave continually updates during the fit to show the fit function evaluated with the current coefficients.
Residual wave	Optional output	The difference between the data and the model.
Weighting wave	Optional input	Used to control how much individual Y data points contribute to the search for the output coefficients.
System variables K0, K1, K2 ...	Input and output	For built-in fit functions only. Optionally takes initial guesses from the system variables and updates them at the end of the fit.
Coefficients wave	Input and Output	Takes initial guesses from the coefficients wave, updates it during the fit and leaves final coefficients in it. See the reference material for CurveFit and FuncFit for additional options.
Epsilon wave	Optional input	For user-defined fit functions only. Used by the curve fitting algorithm to calculate partial derivatives with respect to the coefficients.
W_sigma	Output	Creates this wave and stores the estimates of error for the coefficients in it.
W_fitConstants	Output	Created when you do a fit using a built-in fit function containing a constant. Igor creates this wave and stores the values of any constants used by the fit equation. For details, see Fits with Constants. For notes on constants used in specific fit functions, see Built-in Curve Fitting Functions.
V_<xxx>	Input	There are a number of special variables, such as V_FitOptions, that you can set to tweak the behavior of the curve fitting algorithms.
V_<xxx>	Output	Creates and sets a number of variables such as V_chisq and V_npnts. These contain various statistics found by the curve fit.
M_Covar	Output	Optionally creates a matrix wave containing the "covariance matrix". It can be used to generate advanced statistics.
Other waves	Optional input	User-supplied or automatically and output generated waves for displaying confidence and prediction bands, and for specifying constraints on coefficient values.

Curve Fitting Dialog Tabs

This section describes the controls on each tab and on the main pane of the Curve Fitting dialog.

Global Controls

The controls at the bottom of the dialog are always available:

If you click the Commands radio button, Igor displays the commands generated by the dialog instead of the equation.

Function and Data Tab

The Function and Data tab has a variety of appearances depending on the function selected in the Function menu. Here is what it looks like when the built-in sin function is selected:

Function menu: The main purpose is to select a function to fit.

The menu also has two items that control what functions are displayed in the menu:

Select Show Multivariate functions to include functions of more than one independent variable.

Select Show Old-Style Functions to display functions that lack the FitFunc keyword. See the section User-Defined Fitting Functions for details on the FitFunc keyword. You may need to select this item if you have fitting functions from a version of Igor Pro older than version 4.

Some of the fit functions require additional information that is collected by customized items that appear when you select the function.

Polynomial Terms: Appears when you select the poly function to fit a polynomial. Note that the number of terms is one greater than the degree — set this to three for a quadratic polynomial.

Set Constant X0: Appears when you select the exp_XOffset , dblexp_XOffset or poly_XOffset function. X0 is a constant subtracted from the X values to move the X range for fitting closer to zero. This eliminates numerical problems that arise when evaluating exponentials over X ranges even moderately far from zero. Setting X0 to Auto causes it to be set to the minimum X value in your input data. Setting to a number overrides this default behavior.

Expected Points/Cycle: Appears when you select the sin function. Use it to set the approximate number of data points in one cycle of the sin function. Helps the automatic initial guess come up with good guesses. If it is set to less than four, Igor will use the default of seven.

2D Polynomial Order: Appears when you select the Poly2D function to fit a two-dimensional polynomial (a multivariate function — only appears in the menu when you have selected Show Multivariate Functions). Sets the order of the polynomial, not the number of terms. Because a given order includes a term for X and a term for Y plus cross terms, the number of terms is (N+1)(N+2)/2 where N is the order.

New Fit Function: Click this button to bring up a dialog in which you can define your own fitting function.

Edit Fit Function: This button is available when you have selected a user-defined function from the Function menu. Brings up a dialog in which you can edit your user-defined function.

Y Data: Select a wave containing the dependent variable data to fit. When a multivariate function is selected in the Function menu, the Y Data menu shows1D waves and waves with dimensions matching the number of independent variables used by the function.

X Data: This area changes depending on the function and Y Data wave selected.

With a univariate function, just the X data menu is shown. Select _calculated_ if you have just a Y wave; the X values will come from the Y wave's X scaling. The X Data menu shows only waves with the same number of points as the Y wave.

When a multivariate function and a 1D Y wave are selected, it adds a list box below the X wave menu. You must select one X wave for each independent variable used by the fit function, or a single multicolumn wave with the correct number of columns. As you select X waves, they are added to the list. The order of waves in the list is important — it determines which is identified with each of the function's independent variables.

Remove waves from the list by highlighting a wave and pressing Backspace.

With a multivariate function and a multidimensional Y wave selected, it displays four independent variables wave menus, one for each dimension that a wave can have. Each menu displays waves of length matching the corresponding dimension of the Y Data wave. Select _calculated_ if the independent variable values will come from the Y wave's dimension scaling.

From Target: when From Target is selected, the Y Data and X Data menus show only waves that are displayed in the top table or graph. Makes it easier to find waves in the menus when you are working on an experiment with many waves. When you click the From Target checkbox, it will attempt to select appropriate waves for the X and Y data.

Data Options Tab

Range: Enter point numbers for starting and ending points when fitting to a subset of the Y data.

Historical Note: These boxes used to require X values, they now require point numbers.

Cursors: Available when the top window is a graph displaying the Y data and the graph has the graph cursors on the Y data trace. Click this button to enter text in the Start and End range boxes that will restrict fitting to the data between the graph cursors.

note

If the data use both a Y wave and an X wave, and the X values are in random order, you won't get the expected result.

Clear: Click this button to remove text from the Start and End range boxes.

The range box changes if you have selected a multivariate function and multidimensional Y wave. The dialog presents Start and End range boxes for each dimension of the Y wave.

Weighting: select a wave that contains weighting values. Only waves that match the Y wave in number of points and dimensions are shown in this menu. See Weighting for details.

Wave Contains: select Standard Deviation if the weighting wave contains values of standard deviation for each Y data point. A larger value decreases the influence of a point on the fit.

Select 1/Standard Deviation if your weighting wave contains values of the reciprocal of the standard deviation. A larger value increases the influence of the point on the fit.

Data Mask: select a wave that contains ones and zeroes or NaN's indicating which Y Data points should be included in the fit. Only waves that match the Y wave in number of points and dimensions are shown in this menu. A one indicates a data point that should be included, a zero or NaN (Not a Number or blank in a table) indicates a point that should be excluded.

Coefficients Tab

The coefficients tab is quite complex. It is completely explained in the various sections on how to do a fit. See Two Useful Additions: Holding a Coefficient and Generating Residuals, The Automatic Guesses Didn't Work, The Coefficients Tab for a User-Defined Function, and The Coefficient Wave.

Output Options Tab

The output options tab has settings that control the reporting and display of fit results:

Destination: Select a wave to receive model values from the fit, or select _auto_ to have Igor create an evenly-spaced auto-destination wave for the model values. Updated on each iteration so you can follow the fit progress by the graph display. See The Destination Wave for details on the Destination menu, the Length box shown above and on the New Wave box that isn't shown above.

X Range Full Width of Graph: If you have restricted the range of the fit using graph cursors, the auto destination wave will cover only the range selected. Select this checkbox to make the auto destination cover the full width of the graph.

Residual: Select a wave to receive calculated values of residuals, or the differences between the model and the data. See Computing Residuals for details on residuals and on the various selections you can make from this menu.

Error Analysis: Selects various kinds of statistical error analysis. See Confidence Bands and Coefficient Confidence Intervals for details.

Add Textbox to Graph: When selected, a textbox with information about the fit will be added to the graph containing the Y data. Click the Textbox Preferences button to display a dialog in which you can select various bits of information to be included in the text box.

Create Covariance Matrix: When this is selected, the dialog generates the command to create a covariance matrix for the fit. See Covariance Matrix for details on the covariance matrix.

Suppress Screen Updates: When this is selected, graphs and tables are not updated while the fit progresses. This can greatly speed up the fitting process, especially if the fit involves a contour or image plot, but reduces the feedback you get during the fit.

Computing Residuals

A residual is what is left when you subtract your fitting function model from your raw data.

Ideally, your raw data is equal to some known function plus random noise. If you subtract the function from your data, what's left should be noise. If this is not the case, then the function doesn't properly fit your raw data.

The graphs below illustrate some exponential raw data fitted to an exponential function and to a quadratic (3 term polynomial). The residuals from the exponential fit are random whereas the residuals from the quadratic display a trend overlaid on the random scatter. This indicates that the quadratic is not a good fit for the data.

The easiest way to make a graph such as these is to let it proceed automatically using the Residual pop-up menu in the Output Options tab of the Curve Fitting dialog. The graphs above were made this way with some minor tweaks to improve the display.

The residuals are recalculated at every iteration of a fit. If the residuals are displayed on a graph, you can watch the residuals change as the fit proceeds.

In addition to providing an easy way to compute residuals and add the residual plot to a graph, it prints the wave assignment used to create the residuals into the history area as part of the curve fitting process. For instance, this is the result of a line fit to waveform data:

•CurveFit line LineYData /X=LineXData /D /R
  fit_LineYData= W_coef[0]+W_coef[1]*x
  Res_LineYData= LineYData[p] - (W_coef[0]+W_coef[1]*LineXData[p])
  W_coef={-0.037971,2.9298}
  V_chisq= 18.25;V_npnts= 20;V_numNaNs= 0;V_numINFs= 0;
  V_startRow= 0;V_endRow= 19;V_q= 1;V_Rab= -0.879789;
  V_Pr= 0.956769;V_r2= 0.915408;
  W_sigma={0.474,0.21}
  Coefficient values ± one standard deviation
	a	=-0.037971 ± 0.474
	b	=2.9298 ± 0.21

In this case, a wave called "LineYData" was fit with a straight line model. _auto trace_ was selected for both the destination (/D flag) and the residual (/R flag), so the waves fit_LineYData and Res_LineYData were created. The third line above gives the equation for calculating the residuals. You can copy this line if you wish to recalculate the residuals at a later time. You can edit the line if you want to calculate the residuals in a different way. See Calculating Residuals After the Fit.

Residuals Using Auto Trace

If you select _auto trace_ from the Residual menu, it will automatically create a wave for residual values and, if the Y data are displayed in the top graph, it will append the residual wave to the graph.

The automatically-created residual wave is named by prepending "Res_" to the name of the Y data wave. If the resulting name is too long, it will be truncated. If a wave with that name already exists, it will be reused, overwriting the values already in the wave. If a wave does not exist already, the newly-created wave is automatically filled with NaN. The residual wave is made with the same number of points as the data wave, with one residual value calculated for each data point.

Residual values are stored only for data points that actually participate in fitting. That is, if you fit to a subrange of the data, or use a mask wave to eliminate some points from fitting, residuals are stored only for the data used in fitting and the other points are not disturbed. This allows you to use the auto-residual option to build up the residuals from a piece-wise fit, where parts of the data are fit in succession. It also means that sometimes Igor will leave behind stale values. To prevent that, pre-fill your residual wave with a value of your choice.

If you fit the same data again, the same residual wave will be used. Thus, to preserve a previous result, you must rename the residual wave. This can be done using the Rename item in the Data menu, or the Rename command on the command line.

Residuals are displayed on a stacked graph like those above. This is done by shortening the axis used to display the Y data, and positioning a new free axis above the axis used for the Y data. The residual plot occupies the space made by shortening the data axis. The axis that it creates is given a name derived from the axis used to display the Y data, either "Res_Left" or "Res_Right" if the Y data are displayed on the standard axes. If the data axis is a named free axis, the automatically-generated axis is given a name created by prepending "Res_" to the name of the data axis.

Igor tries hard to make the appended residual plot look nice by copying the formatting of the Y data trace and making the residual trace identical so that you can tell which residual trace goes with a given Y data trace. The axis formatting for the residual axis is copied from the vertical axis used for the data trace, and the residual axis is positioned directly above the data axis. Any other vertical axes that might be in the way are also shortened to make room. Here are two examples of graphs that have been modified by the auto-trace residuals:

It is likely that the automatic formatting won't be quite what you want, but it will probably be close enough that you can use the Modify Axis and Modify Trace Appearance dialogs to tweak the formatting. For details see the Graphs help file and especially the topics Creating Graphs With Multiple Axes and Creating Stacked Plots.

Removing the Residual Auto Trace

When an auto-trace residual plot is added to a graph, it modifies the axis used to plot the original Y data. If you remove the auto-trace residual from the graph, the residual axis is removed and in most cases the Y data axis is restored to its previous state.

In some complicated graphs the restoration of the data axis isn't done correctly. To restore the graph, double-click the Y data axis to bring up the Modify Axes dialog and select the Axis tab. You will find two settings labeled "Draw between ... and ... % of normal". Typically, the correct settings will be 0 and 100.

Residuals Using Auto Wave

Because the changes to the graph formatting are substantial, you may want the automatic residual wave created and filled in but not appended to the graph. To accomplish this, simply choose _Auto Wave_ from the Residual pop-up menu in the Curve Fitting dialog. Once the wave is made by the curve fitting process, you can append it to a graph, or use it in any other way you wish.

Residuals Using an Explicit Residual Wave

You can select a wave from the Residual pop-up menu and that wave will be filled with residual values. In this case, it does not append the wave to the top graph. You can use this technique to make graphs with the formatting completely under your own control, or to use the residuals for some other purpose.

Only waves having the same number of points as the Y data wave are listed in the menu. If you don't want to let the dialog create the wave, you would first create a suitable wave by duplicating the Y data wave using the Duplicate Waves item in the Data menu, or using the Duplicate command:

Duplicate yData, residuals_poly3

It is often a good idea to set the wave to NaN, especially when fitting to a subrange of the data:

residuals_poly3=NaN

After the wave is duplicated, it would typically be appended to a graph or table before it is used in curve fitting.

Explicit Residual Wave Using New Wave

The easiest way to make an explicit residual wave is to let the Curve Fitting dialog do it for you. You do this by selecting _New Wave_ in the Residual menu. A box appears allowing you to enter a name for the new wave. The dialog will then generate the required commands to make the wave before the curve fit starts. The wave made this way will not be added to a graph. You will need to do that yourself after the fit is finished.

Calculating Residuals After the Fit

You may wish to avoid the overhead of calculating residuals during the fitting process. This section describes ways to calculate the residuals after a curve fit without depending on automatic wave creation.

Graphs similar to the ones at the top of this section can be made by appending a residuals wave using a free left axis. Then, under the Axis tab of the Modify Axes dialog, the distance for the free axis was set to zero and the axis was set to draw between 80 and 100% of normal. The normal left axis was set to draw between 0 and 70% and axis standoff was turned off for both left and bottom axes.

Here are representative commands used to accomplish this.

// Make sample data
Make/N=500 xData, yData
xData = x/500 + gnoise(1/1000)
yData = 100 + 1000*exp(-.005*x) + gnoise(20)

// Do exponential fit with auto-trace
CurveFit exp yData /X=xData /D
Rename fit_yData, fit_yData_exp

// Calculate exponential residuals using interpolation in
// the auto trace wave to get model values
Duplicate yData, residuals_exp
residuals_exp = yData - fit_yData_exp(xData)

// Do polynomial fit with auto-trace
CurveFit poly 3, yData /X=xData /D
Rename fit_yData fit_yData_poly3

// Find polynomial residuals
Duplicate yData, residuals_poly3
residuals_poly3 = yData - fit_yData_poly3(xData)

Calculating model values by interpolating in the auto trace wave may not be sufficiently accurate. Instead, you can calculate the exact value using the actual fitting expression. When the fit finishes, it prints the equation for the fit in the history. With a little bit of editing you can create a wave assignment for calculating residuals. Here are the assignments from the history for the above fits:

fit_yData= poly(W_coef,x)
fit_yData= W_coef[0]+W_coef[1]*exp(-W_coef[2]*x)

We can convert these into residuals calculations like this:

residuals_poly3 = yData - poly(W_coef,xData)
residuals_exp = yData - (W_coef[0]+W_coef[1]*exp(-W_coef[2]*xData))

Note that we replaced "x" with "xData" because we have tabulated x values. If we had been fitting equally spaced data then we would not have had a wave of tabulated x values and would have left the "x" alone.

This technique for calculating residuals can also be used if you create and use an explicit destination wave. In this case the residuals are simply the difference between the data and the destination wave. For example, we could have done the exp fit and residual calculations as follows:

Duplicate yData, yDataExpFit,residuals_exp
// explicit destination wave using /D=wave
CurveFit exp yData /X=xData /D=yDataExpFit
residuals_exp = yData - yDataExpFit

Coefficient of Determination or R-Squared

When you do a line fit, y = a + bx, Igor prints a variety of statistics, including "r-squared", also known as the "coefficient of determination". The value of r-squared is stored in the automatically-created variable V_r2.

The literature on regression shows differences of opinion on the interpretation of r-squared. Because it is commonly reported, Igor provides the value.

There are two ways to compute r-squared that reflect slightly different interpretations:


$\displaystyle r^{2}=1-\frac{S S_{r e s}}{S S_{t o t}}$	(1)
$\displaystyle r^{2}=\frac{S S_{r e g}}{S S_{t o t}}$	(2)

where


$\displaystyle S S_{t o t}=\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}$	(3 - total sum of squares)
$\displaystyle S S_{\text {res }}=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}$	(4 - residual sum of squares)
$\displaystyle S S_{ {reg }}=\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2}$	(5 - regression sum of squares)

Here, y_i is the i-th Y data point, ŷ_i is i-th predicted or model Y value, and y̅_i is the average of the Y data. When you do a line fit, the fit line is guaranteed to pass through the data average, and you can be sure that

SS_tot = SS_res + SS_reg (6)

Consequently, equations (1) and (2) are equivalent, with equation (2) emphasizing the interpretation of r-squared as "explained variance". That is, it is the fraction of the data variance that is "explained" or accounted for by the fit line. The r-squared value reported by Igor generally agrees with values from Excel and other applications.

Igor also reports the Pearson correlation coeffient via the automatically-created variable V_Pr. In the case of a line fit, V_Pr² = V_r2.

R-Squared and Fits Through the Origin

The situation changes if you fit a line that is constrained to pass through the origin, that is, you set the value of the fit coefficient a to zero and hold it. This is usually done when common sense or theory demands that the quantity of interest must be zero at X=0.

There is no consensus on the correct way to compute something like r-squared for a line fit through the origin. Such a fit does not, in general, pass through the average data value, and equation (6) does not hold, so equations (1) and (2) do not give the same value.

We prefer the interpretation of r-squared as "explained variance" so we use equation (2) for fits through the origin. This has some consequences. One is that Igor's r-squared will not necessarily agree with other applications, notably Excel. Another is that it is guaranteed to be smaller, some would say, "less good", than a line fit to the same data that is not constrained to pass through the origin.

A more surprising consequence is that it is possible for r-squared to be larger than 1. This has a simple interpretation: your fit line has larger variance than the data! Quite possibly a fit through the origin is simply not justified for your data.

Given the lack of consensus and uncertain interpretation of r-squared for a fit through the origin, we cannot recommend citing it, or using it as any sort of indication of goodness of fit, for such fits.

Estimates of Error

Igor automatically calculates the estimated error (standard deviation) for each of the coefficients in a curve fit. When you perform a curve fit, it creates a wave called W_sigma. Each point of W_sigma is set to the estimated error of the corresponding coefficients in the fit. The estimated errors are also indicated in the history area, along with the other results from the fit. If you don't provide a weighting wave, the sigma values are estimated from the residuals. This implicitly assumes that the errors are normally distributed with zero mean and constant variance and that the fit function is a good description of the data.

The coefficients and their sigma values are estimates (usually remarkably good estimates) of what you would get if you performed the same fit an infinite number of times on the same underlying data (but with different noise each time) and then calculated the mean and standard deviation for each coefficient.

Confidence Bands and Coefficient Confidence Intervals

You can graphically display the uncertainty of a model fit to data by adding confidence bands or prediction bands to your graph. These are curves that show the region within which your model or measured data are expected to fall with a certain level of probability. A confidence band shows the region within which the model is expected to fall while a prediction band shows the region within which random samples from that model plus random errors are expected to fall.

You can also calculate a confidence interval for the fit coefficients. A confidence interval estimates the interval within which the real coefficient will fall with a certain probability.

note

Confidence and prediction bands are not available for multivariate curve fits.

You control the display of confidence and prediction bands and the calculation of coefficient confidence intervals using the Error Analysis section of the Output Options tab of the Curve Fitting dialog:

Using the line fit example at the beginning of this help file (see A Simple Case -- Fitting to a Built-in Function: Line Fit), we set the confidence level to 95% and selected all three error analysis options to generate this output and graph:

•CurveFit line LineYData /X=LineXData /D /F={0.950000, 7}
  fit_LineYData= W_coef[0]+W_coef[1]*x
  W_coef={-0.037971,2.9298}
  V_chisq= 18.25; V_npnts= 20; V_numNaNs= 0; V_numINFs= 0;
  V_startRow= 0; V_endRow= 19; V_q= 1; V_Rab= -0.879789;
  V_Pr= 0.956769;V_r2= 0.915408;
  W_sigma={0.474,0.21}
  Fit coefficient confidence intervals at 95.00% confidence level:
  W_ParamConfidenceInterval={0.995,0.441,0.95}
  Coefficient values ± 95.00% Confidence Interval
   a = -0.037971 ± 0.995
   b = 2.9298 ± 0.441

You can do this with nonlinear functions also, but be aware that it is only an approximation for nonlinear functions:

Make/O/N=100 GDataX, GDataY                     // waves for data
GDataX = enoise(10)                             // Random X values
GDataY = 3*exp(-((GDataX-2)/2)^2) + gnoise(0.3) // Gaussian plus noise
Display GDataY vs GDataX                        // graph the data
ModifyGraph mode=2,lsize=2                      // as dots
CurveFit Gauss GDataY /X=GDataX /D/F={.99, 3}

The dialog supports only automatically-generated waves for confidence bands. The CurveFit and FuncFit operations support several other options including an error bar-style display. See CurveFit for details.

Calculating Confidence Intervals After the Fit

You can use the values from the W_sigma wave to calculate a confidence interval for the fit coefficients after the fit is finished. Use the StudentT function to do this. The following information was printed into the history following a curve fit:

Fit converged properly
fit_junk= f(coeffs,x)
coeffs={4.3039,1.9014}
V_chisq= 101695; V_npnts= 128; V_numNaNs= 0; V_numINFs= 0;
W_sigma={4.99,0.0679}

To calculate the 95 per cent confidence interval for fit coefficients and deposit the values into another wave, you could execute the following lines:

Duplicate W_sigma, ConfInterval
ConfInterval = W_sigma[p]*StudentT(0.95, V_npnts-numpnts(coeffs))

Naturally, you could simply type "126" instead of "V_npnts-numpnts(coeffs)", but as written the line will work unaltered for any fit. When we did this following the fit in the example, these were the results:

ConfInterval = {9.86734,0.134469}

Clearly, coeffs[0] is not significantly different from zero.

Confidence Band Waves

New waves containing values required to display confidence and prediction bands are created by the curve fit if you have selected these options. The number of waves and the names depend on which options are selected and the style of display. For a contour band, such as shown above, there are two waves: one for the upper contour and one for the lower contour. Only one wave is required to display error bars. For details, see the CurveFit operation.

Some Statistics

Calculation of the confidence and prediction bands involve some statistical assumptions. First, of course, the measurement errors are assumed to be normally distributed. Departures from normality usually have to be fairly substantial to cause real problems.

If you don't supply a weighting wave, the distribution of errors is estimated from the residuals. In making this estimate, the distribution is assumed to be not only normal, but also uniform with mean of zero. That is, the error distribution is centered on the model and the standard deviation of the errors is the same for all values of the independent variable. The assumption of zero mean requires that the model be correct; that is, it assumes that the measured data truly represent the model plus random normal errors.

Some data sets are not well characterized by the assumption that the errors are uniform. In that case, you should specify the error distribution by supplying a weighting wave (see Weighting). If you do this, your error estimates are used for determining the uncertainties in the fit coefficients, and, therefore, also in calculating the confidence band.

The confidence band relies only on the model coefficients and the estimated uncertainties in the coefficients, and will always be calculated taking into account error estimates provided by a weighting wave. The prediction band, on the other hand, also depends on the distribution of measurement errors at each point. These errors are not taken into account, however, and only the uniform measurement error estimated from the residuals are used.

The calculation of the confidence and prediction bands is based on an estimate of the variance of a predicted model value:

\displaystyle \begin{aligned} V(\hat{Y}) & =a^{T} C a \\ a & =\delta F /\left.\delta p\right|_{x} \end{aligned}

Here, Ŷ is the predicted value of the model at a given value of the independent variable X, a is the vector of partial derivatives of the model with respect to the coefficients evaluated at the given value of the independent variable, and C is the covariance matrix. Often you see the a^TCa term multiplied by σ², the sample variance, but this is included in the covariance matrix. The confidence interval and prediction interval are calculated as:

\displaystyle C I=t(n-p, 1-\alpha / 2)[V(\hat{Y})]^{1 / 2} \text { and } P I=t(n-p, 1-\alpha / 2)\left[\sigma^{2}+V(\hat{Y})\right]^{1 / 2} .

The quantities calculated by these equations are the magnitudes of the intervals. These are the values used for error bars. These values are added to the model values (Ŷ) to generate the waves used to display the bands as contours. The function t(n -p, 1-α/2) is the point on a Student's t distribution having probability 1-α/2, and σ² is the sample variance. In the calculation of the prediction interval, the value used for σ² is the uniform value estimated from the residuals. This is not correct if you have supplied a weighting wave with nonuniform values because there is no information on the correct values of the sample variance for arbitrary values of the independent variable. You can calculate the correct prediction interval using the StudentT function. You will need a value of the derivatives of your fitting function with respect to the fitting coefficients. You can either differentiate your function and write another function to provide derivatives, or you can use a numerical approximation. Igor uses a numerical approximation.

Confidence Bands and Nonlinear Functions

Strictly speaking, the discussion and equations above are only correct for functions that are linear in the fitting coefficients. In that case, the vector a is simply a vector of the basis functions. For a polynomial fit, that means 1, x, x², etc. When the fitting function is nonlinear, the equation results from an approximation that uses only the linear term of a Taylor expansion. Thus, the confidence bands and prediction bands are only approximate. It is impossible to say how bad the approximation is, as it depends heavily on the function.

Covariance Matrix

If you select the Create Covariance Matrix checkbox in the Output Options tab of the Curve Fitting dialog, it generates a covariance matrix for the curve fitting coefficients. This is available for all of the fits except the straight-line fit. Instead, a straight-line fit generates the special output variable V_rab giving the coefficient of correlation between the slope and Y intercept.

By default (if you are using the Curve Fitting dialog) it generates a matrix wave having N rows and columns, where N is the number of coefficients. The name of the wave is M_Covar. This wave can be used in matrix operations. If you are using the CurveFit, FuncFit or FuncFitMD operations from the command line or in a user procedure, use the /M=2 flag to generate a matrix wave.

Originally, curve fits created one 1D wave for each fit coefficient. The waves taken all together made up the covariance matrix. For compatibility with previous versions, the /M=1 flag still produces multiple 1D waves with names W_Covarn. Please don't do this on purpose.

The diagonal elements of the matrix, M_Covar[i][i], are the variances for parameter i. The variance is the square of sigma, the standard deviation of the estimated error for that parameter.

The covariance matrix is described in detail in Numerical Recipes in C, edition 2, page 685 and section 15.5. Also see the discussion under Weighting.

Correlation Matrix

Use the following commands to calculate a correlation matrix from the covariance matrix produced during a curve fit:

Duplicate M_Covar, CorMat	 // You can use any name instead of CorMat
CorMat = M_Covar[p][q]/sqrt(M_Covar[p][p]*M_Covar[q][q])

A correlation matrix is a normalized form of the covariance matrix. Each element shows the correlation between two fit coefficients as a number between -1 and 1. The correlation between two coefficients is perfect if the corresponding element is 1, it is a perfect inverse correlation if the element is -1, and there is no correlation if it is 0.

You should be suspicious of fits in which an element of the correlation matrix is very close to 1 or -1. This may signal "identifiability" problems. That is, the fit doesn't distinguish between two of the parameters very well, and so the fit isn't very well constrained. Sometimes a fit can be rewritten with new parameters that are combinations of the old ones to get around this problem.

Identifiability Problems

In addition to off-diagonal elements of the correlation matrix that are near 1 or -1, symptoms of identifiability problems include fits that require a large number of iterations to converge, or fits in which the estimated coefficient errors (W_sigma wave) are unreasonably large.

The phrase "identifiability problems" describes a situation in which two or more of the fit coefficients trade off in a way that makes it nearly impossible to solve for the values of both at once. They are correlated in a way that if you adjust one coefficient, you can find a value of the other that makes a fit that is nearly as good.

When the correlation is too strong, the fitting algorithm doesn't know where to go and therefore wanders around in a coefficient space in which a broad range of values all seem about as good. That is, broad regions in chi-square space provide very little variation in chi-square. The usual result is apparent convergence but with large estimated values in W_sigma, or a singular matrix error.

The error estimates are based on the curvature of the chi-square surface around the solution point. A flat-bottomed chi-square surface, such as results from having many solutions that are nearly as good, results in large errors. The flat bottom of the chi-square surface also results in small derivatives with respect to the coefficients that don't give a good indication of where the fit should go next, so iterations wander around, giving rise to fits that require many iterations to converge.

If you see a fit with unreasonably large error estimates, or that take many iterations to converge, compute the correlation matrix and look for off-diagonal values near 1 or -1. In our experience, values about 0.9 are probably OK. Values near 0.99 are suspicious but can be acceptable. Values around 0.999 are almost certainly an indication of problems.

Unfortunately, there is little you can do about identifiability problems. It is a mathematical characteristic of your fitting function. Sometimes a model has regions in coefficient space where two coefficients have similar effects on a fit, and expanding the range of the independent variable can alleviate the problem. Occasionally some feature controlled by a coefficient might be very narrow and you can fix the problem with higher sampling density.

Fitting with Constraints

It is sometimes desirable to restrict values of the coefficients to a fitting function. Sometimes fitting functions may allow coefficient values that, while fine mathematically, are not physically reasonable. At other times, some ranges of coefficient values may cause mathematical problems such as singularities in the function values, or function values that are so large that they overflow the computer representation. In such cases it is often desirable to apply constraints to keep the solution out of the problem areas. It could be that the final solution doesn't involve any active constraints, but the constraints prevent termination of the fit on an error caused by wandering into bad regions on the way to the solution.

Curve fitting supports constraints on the values of any linear combination of the fit coefficients. The Curve Fitting dialog supports constraints on the value of individual coefficients.

The algorithm used to apply constraints is quite forgiving. Your initial guesses do not have to be within the constraint region (that is, initial guesses are allowed to violate the constraints). In most cases, it will simply move the parameters onto a boundary of the constraint region and proceed with the fit. The constraints can even be contradictory ("infeasible" in the curve fitting jargon) so long as the violations aren't too severe, and the fit will simply "split the difference" to give you coefficients that are a compromise amongst the infeasible constraints.

Constraints are not available for the built-in line, poly and poly2D fit functions. To apply constraints to these fit functions you must create a user-defined fit function.

Constraints Using the Curve Fitting Dialog

The Coefficients Tab of the Curve Fitting dialog includes a menu to enable fitting with constraints. When you select the checkbox, the constraints section of the Coefficients list becomes available:

Filling in a value in the Lower Constraint column generates a command to constrain the corresponding coefficient to values greater than the value you enter. Filling in a value in the Upper Constraint column constrains the corresponding coefficient to values less than the value you enter. A box that is left empty does not generate any constraint.

The figure above was made with the gauss function selected. The following commands are generated by the dialog:

Make/O/T/N=2 T_Constraints
T_Constraints[0] = {"K2 > 40","K2 < 60"}
CurveFit gauss aa /D /C=T_Constraints

More complicated constraints are possible, but cannot be entered in the Curve Fitting dialog. This requires that you make a constraints wave before you enter the dialog. Then select the wave from the Constraints menu. See the following sections to learn how to construct the constraints wave.

Complex Constraints Using a Constraints Wave

You can constrain the values of linear combinations of coefficients, but the Curve Fitting dialog provides support only for simple constraints. You can construct an appropriate text wave with constraints before entering the Curve Fitting dialog. Select the wave from the Constraints menu in the Coefficients tab. You can also use the CurveFit or FuncFit commands on the command line with a constraints wave.

Each element of the text wave holds one constraint expression. Using a text wave makes it easy to edit the expressions in a table. Otherwise, you must use a command line like the second line in the example shown above.

Constraint Expressions

Constraint expressions can be arbitrarily complex, and can involve any or all of the fit coefficients. Each expression must have an inequality symbol ("<", "<=", ">", or ">="). In the expressions the symbol Kn (K0, K1, etc.) is used to represent the nth fitting coefficient. This is like the Kn system variables, but they are merely symbolic place holders in constraint expressions. Expressions can involve sums of any combination of the Kn's and factors that multiply or divide the Kn's. Factors may be arbitrarily complex, even nonlinear, as long as they do not involve any of the Kn's. The Kn's cannot be used in a call to a function, and cannot be involved in a nonlinear expression. Here are some legal constraint expressions:

K0 > 5
K1+K2 < numVar^2+2					// numVar is a global numeric variable
K0/5 < 2*K1
(numVar+3)*K3 > K1+K2/(numVar-2)
log(numVar)*K3 > 5					// nonlinear factor doesn't involve K3

These are not legal:

K0*K1 > 5								// K0*K1 is nonlinear
1/K1 < 4								// This is nonlinear: division by K1
ln(K0) < 1								// K0 not allowed as parameter to a function

When constraint expressions are parsed, the factors that multiply or divide the Kn's are extracted as literal strings and evaluated separately. Thus, if you have <expression>*K0 or K0/<expression>, <expression> must be executable on its own.

You cannot use a text wave with constraint expressions for fitting from a thread-safe function. You must use the method described in Constraint Matrix and Vector.

Equality Constraint

You may wish to constrain the value of a fit coefficient to be equal to a particular value. The constraint algorithm does not have a provision for equality constraints. One way to fake this is to use two constraints that require a coefficient to be both greater than and less than a value. For instance, "K1 > 5" and "K1 < 5" will require K1 to be equal to 5.

If it is a single parameter that is to be held equal to a value, this isn't the best method. You are much better off holding a parameter. In the Curve Fitting dialog, simply select the Hold box in the Coefficients list on the Coefficients tab and enter a value in the Initial Guess column. If you are using a command line to do the fit,

FuncFit/H="01"...

will hold K1 at a particular value. Note that you have to set that value before starting the fit.

Example Fit with Constraints

You can execute the example commands in the help file by selecting the line or lines and pressing Ctrl+Enter.

This example fits to a sum of two exponentials, while constraining the sum of the exponential amplitudes to be less than some limit that might be imposed by theoretical knowledge. We use the command line because the constraint is too complicated to enter into the Curve Fitting dialog.

First, make the data and graph it:

Make/O/N=50 expData= 3*exp(-0.2*x) + 3*exp(-0.03*x) + gnoise(.1)
Display expData
ModifyGraph mode=3,marker=8

Do a fit without constraints:

CurveFit dblExp expData /D/R

The following command makes a text wave with a single element containing the string "K1 + K3 < 5" which implements a restriction on the sum of the individual exponential amplitudes.

Make/O/T CTextWave={"K1 + K3 < 5"}

The wave is made using commands so that it could be written into this help file. It may be easier to use the Make Waves item from the Data menu to make the wave, and then display the wave in a table to edit the expressions. Make sure you make Text wave. Do not leave any blank lines in the wave.

Now do the fit again with constraints:

CurveFit dblExp expData /D/R/C=CTextWave

In this case, the difference is slight; in the graph of the fit with constraints, notice that the fit line is slightly lower at the left end and slightly higher at the right end than in the standard curve fit, and that difference is reflected in the residual values at the ends:

The output from a curve fit with constraints includes these lines reporting on the fact that constraints were used, and that the constraint was active in the solution:

--Curve fit with constraints--
  Active Constraint: Desired:  K1+K3<5  Achieved:  K1+K3=5

In most cases you will see a message similar to this one. If you have conflicting constraints, it is likely that one or more constraints will be violated. In that case, you will get a report of that fact. The following commands add two more constraints to the example. The new constraints require values for the individual amplitudes that sum to a number greater than 5, while still requiring that the sum be less than 5 (so these are "infeasible constraints"):

Make/O/T CTextWave={"K1 + K3 < 5", "K1 > 3.3", "K3 > 2.2"}
CurveFit dblExp expData /D/R/C=CTextWave

In most cases, you would have added the new constraints by editing the constraint wave in a table:

The curve fit report shows that all three constraints were violated in order to achieve a solution:

--Curve fit with constraints--
	Constraint VIOLATED:    Desired:  K1>3.3  Achieved:  K1=3.06604
	Constraint VIOLATED:    Desired:  K3>2.2  Achieved:  K3=1.93381

Constraint Matrix and Vector

When you do a constrained fit, it parses the constraint expressions and builds a matrix and a vector that describe the constraints.

Each constraint expression is parsed to form a simple expression like

C₀K₀ + C₁K₁ + . . . <= D,

where the K_i's are the fit coefficients, and the C_i's and D are constants. The constraints can be expressed as the matrix operation CK <= D, where C is a matrix of constants, K is the fit coefficient vector, and D is a vector of limits. The matrix has dimensions N by M where N is the number of constraint expressions and M is the number of fit coefficients. In most cases, almost all the elements of the matrix are zeroes. In the previous example, the C matrix and D vector are:

    C matrix          D vector
 1   0   1   0        5
-1   0   0   0       -3.3
 0   0  -1   0       -2.2

This is the form used internally by the curve-fitting code. If you wish, you can build a matrix wave and one-dimensional wave containing the C and D constants. Instead of using /C=textwave to request a fit with constraints, use /C={matrix, 1Dwave}.

In general, it is confusing and error-prone to create the right waves for a given set of constraints. However, it is not allowed to use the textwave method for curve fitting from a threadsafe function (see Constraints and ThreadSafe Functions). Fortunately, Igor can create the necessary waves when it parses the expressions in a text wave.

You create waves containing the C matrix and D vector using the /C flag (note that this flag goes right after the CurveFit command name, not at the end). If you have executed the examples above, you can now execute the following commands to build the waves and display them in a table:

CurveFit/C dblExp expData /D/R/C=CTextWave
Edit M_FitConstraint, W_FitConstraint

The C matrix is named M_FitConstraint and the D vector is named W_FitConstraint (by convention, matrix names start with "M_", 1D wave names start with "W_").

In addition to their usefulness for specifying constraints in a threadsafe function, you can use these waves later to check the constraints. The following commands multiply the generated fit coefficient wave (W_coefs) by the constraint matrix and appends the result to the table made previously:

MatrixMultiply M_FitConstraint, W_coef
AppendToTable M_Product

The result of the MatrixMultiply operation is the matrix wave M_Product. Note that the values of M_Product[1] and M_Product[2] are larger than the corresponding values in W_FitConstraint because the constraints were infeasible and resulted in constraint violations.

Constrained Curve Fitting Pitfalls

Bad Values on the Constraint Boundary

The most likely problem with constrained curve fitting is a value on a constraint boundary that generates a singular matrix error during the curve fit. For instance, it would be reasonable in many applications to require a pre-exponential multiplier to be positive, in this case K₁>0:

\displaystyle y=K_{0}+K_{1} e^{K_{2} x}

It would be natural to write a constraint expression "K1 > 0", but this can lead to problems. If some iteration tries a negative value of K1, the constraints will set K1 to be exactly zero. But when K1 is zero, the function has no dependence on K2 and a singular matrix error results. The solution is to use a constraint that requires K1 to be greater than some small positive number: "K1 > 0.1", for instance. The value of the limit must be tailored to your application. If you expect the constraint to be inactive when the solution is found, and the fit reports that the constraint was active, you can decrease the limit and do the fit again.

Severe Constraint Conflict

Although the method used for applying the constraints can find a solution even when constraints conflict with each other (are infeasible), it is possible to have a conflict that is so bad that the method fails. This will result in a singular matrix error.

Constraint Region is a Poor Fit

It is possible that the region of coefficients space allowed by the constraints is such a bad fit to the data that a singular matrix error results.

Initial Guesses Far Outside the Constraint Region

Usually if the initial guesses for a fit lie outside the region allowed by the constraints, the fit coefficients will shift into the constraint region on the first iteration. It is possible, however, for initial guesses to be so far from the constraint region that the solution to the constraints fails. This will cause the usual singular matrix error.

Constraints Conflict with a Held Parameter

You cannot hold a parameter and apply a constraint to the same parameter. Thus, this is not allowed:

Make/T CWave="K1 > 5"
FuncFit/H="01" myFunc, myCoefs, myData /C=CWave

Constraints Demo

Open Constraint Demo.

NaNs and INFs in Curve Fits

Curve fits ignore NaNs and INFs in the input data. This is a convenient way to eliminate individual data values from a fit. A better way is to use a data mask wave (see Using a Mask Wave).

Special Variables for Curve Fitting

There are a number of special variables used for curve fitting input (to provide additional control of the fit) and for output (to provide additional statistics). Knowledgeable users can use the input variables to tweak the fitting process. However, this is usually not needed. Some output variables help users knowledgeable in statistics to evaluate the quality of a curve fit.

To use an input variable interactively, create it from the command line using the Variable operation before performing the fit.

Most of the output variables are automatically created by the CurveFit or FuncFit operations. Some, as indicated below, are not automatically created; you must create them yourself if you want the information they provide.

Unless otherwise specified, the output variables are created if they don't already exist. Some of them are printed in the history.

If you perform a curve fit in a procedure, both the input and output variables can be local or global. It is best to make them local. See Accessing Variables Used by Igor Operations for information on how to use local variables. In procedures, output-only variables are always created as local variables.

If you perform a curve fit interactively via the command line or via the Curve Fitting dialog, the variables will be global. If you use multiple data folders (described in Data Folders), you need to remember that input and output variables are searched for or created in the current data folder.

The following table lists all of the input and output special variables. Some of them are discussed in more detail below.

Variable	I/O	Meaning
V_FitOptions	Input	Miscellaneous options for curve fit.
V_FitTol	Input	Normally, an iterative fit terminates when the fractional decrease of chi-square from one iteration to the next is less than 0.001. If you create a global variable named V_FitTol and set it to a value between 1E-10 and 0.1 then that value will be used as the termination tolerance. Values outside that range will have no effect.
V_tol	Input	(poly fit only) The "singular value threshold". See Special Considerations for Polynomial Fits below.
V_chisq	Output	A measure of the goodness of fit. It has absolute meaning only if you've specified a weighting wave containing the reciprocal of the standard error for each data point.
V_q	Output	(line fit only) A measure of the believability of chi-square. Valid only if you specified a weighting wave.
V_siga, V_sigb	Output	(line fit only) The probable uncertainties of the intercept (K0 = a) and slope (K1 = b) coefficients for a straight-line fit (to y = a + bx).
V_Rab	Output	(line fit only) The coefficient of correlation between the uncertainty in a (the intercept, K0) and the uncertainty in b (the slope, K1).
V_Pr	Output	(line fit only) The linear correlation coefficient r (also called Pearson's r). Values of +1 or -1 indicate complete correlation while values near zero indicate no correlation.
V_r2	Output	(line fit only) The coefficient of determination, usually called simply "r-squared". See Coefficient of Determination or R-Squared for details.
V_npnts	Output	The number of points that were fitted. If you specified a weighting wave then points whose weighting was zero are not included in this count. Also not included are points whose values are NaN or INF.
V_nterms	Output	The number of coefficients in the fit.
V_nheld	Output	The number of coefficients held constant during the fit.
V_numNaNs	Output	The number of NaN values in the data being fit. NaNs are ignored during a curve fit.
V_numINFs	Output	The number of INF values in the data being fit. NaNs are ignored during a curve fit.
V_FitError	I/O	Used from a procedure to attempt to recover from errors during the fit.
V_FitQuitReason	Output	Provides additional information about why a nonlinear fit stopped iterating.
		note You must create this variable; it is not automatically created.
V_FitIterStart	Output	Use of V_FitIterStart is obsolete; use all-at-once fit functions instead. See All-At-Once Fitting Functions for details.
		Set to 1 when an iteration starts. Identifies when the user-defined fitting function is called for the first time for a particular iteration.
		note You must create this variable; it is not automatically created.
V_FitMaxIters	Input	Controls the maximum number of passes without convergence before stopping the fit. By default this is 40. You can set V_FitMaxIters to any value greater than 0. If V_FitMaxIters is less than 1 the default of 40 is used.
V_FitNumIters	Output	Number of iterations.
		note You must create this variable; it is not automatically created.
S_Info	Output	Keyword-value pairs giving certain kinds of information about the fit.
		note You must create this variable; it is not automatically created.

V_FitOptions

There are a number of options that you can invoke for the fitting process by creating a variable named V_FitOptions and setting various bits in it. Set V_FitOptions to 1 to set Bit 0, to 2 to set Bit 1, etc.

Bit 0: Controls X Scaling of Auto-trace Wave

If V_FitOptions exists and has bit 0 set (Variable V_fitOptions=1) and if the Y data wave is on the top graph then the X scaling of the auto-trace destination wave is set to match the appropriate x axis on the graph. This is useful when you want to extrapolate the curve outside the range of x data being fit.

A better way to do this is with the /X flag (not parameter- this flag goes immediately after the CurveFit or FuncFit operation and before the fit function name). See CurveFit for details.

Bit 1: Robust Fitting

You can get a form of robust fitting where the sum of the absolute deviations is minimized rather than the squares of the deviations, which tends to de-emphasize outlier values. To do this, create V_FitOptions and set bit 1 (Variable V_fitOptions=2).

warning

No attempt to adjust the results returned for the estimated errors or for the correlation matrix has been made. You are on your own.

warning

Don't set this bit and then forget about it.

warning

Setting Bit 1 has no effect on line, poly or poly2D fits.

Bit 2: Suppresses the Curve Fit Window

Normally, an iterative fit puts up an informative window while the fit is in progress. If you don't want this window to appear, create V_FitOptions and set bit 2 (Variable V_fitOptions=4). This may speed things up a bit if you are performing batch fitting on a large number of data sets.

A better way to do this is via the /W=2 flag. See CurveFit for details.

Bit 3: Save Iterates

It is sometimes useful to know the path taken by a curve fit getting to a solution (or failing to). To save his information, create V_FitOptions and set bit 3 (Variable V_FitOptions=8). This creates a matrix wave called M_iterates, which contains the values of the fit coefficients at each iteration. The matrix has a row for each iteration and a column for each fit coefficient. The last column contains the value of chi square for each iteration.

Bit 4: Suppress Screen Updates

Works just like setting the /N=1 flag. See CurveFit for details.

Added in Igor Pro 7.00.

Bit 5: Errors Only

When set, just like setting /O flag (Guess only) but for FuncFit also computes the W_sigma wave and optionally the covariance matrix (/M flag) for your set of coefficients. There is the possibility that setting this bit can generate a singular matrix error.

Added in Igor Pro 7.00.

V_chisq

V_chisq is a measure of the goodness of fit. It has absolute meaning only if you've specified a weighting wave. See the discussion in the section Weighting.

V_q

V_q (straight-line fit only) is a measure of the believability of chi-square. It is valid only if you specified a weighting wave. It represents the quantity q which is computed as follows:

q = gammq((N-2)/2, chisq/2)

where gammq is the incomplete gamma function 1-P(a,x) and N is number of points. A q of 0.1 or higher indicates that the goodness of fit is believable. A q of 0.001 indicates that the goodness of fit may be believable. A q of less than 0.001 indicates systematic errors in your data or that you are fitting to the wrong function.

V_FitError and V_FitQuitReason

When an error occurs during a curve fit, it normally causes any running user-defined procedure to abort.

This makes it impossible for you to write a procedure that attempts to recover from errors. However, you can prevent an abort in the case of certain types of errors that arise from unpredictable mathematical circumstances. Do this by creating a variable named V_FitError and setting it to zero before performing a fit. If an error occurs during the fit then it will set bit 0 of V_FitError. Certain errors will also cause other bits to be set in V_FitError:

Error	Bit set
Any error	0
Singular matrix	1
Out of memory	2
Function returned NaN or INF	3
Fit function requested stop	4
Reentrant curve fitting	5

Reentrant curve fitting means that somehow a second curve fit started execution when there was already one running. That could happen if your user-defined fit function tried to do a curve fit, or if a button action procedure that does a fit responded too soon to another click.

There is more than one reason for a fit to stop iterating without an error. To obtain more information about the reason that a nonlinear fit stopped iterating, create a variable named V_FitQuitReason. After the fit, V_FitQuitReason is zero if the fit terminated normally, 1 if the iteration limit was reached, 2 if the user stopped the fit, or 3 if the limit of passes without decreasing chi-square was reached.

Other types of errors, such as missing waves or too few data points for the fit, are likely to be programmer errors. V_FitError does not catch those errors, but you can still prevent an abort if you wish, using the special function AbortOnRTE and Igor's try-catch-endtry construct. Here is an example function that attempts to do a curve fit to a data set that may contain nothing but NaNs:

Function PreventCurveFitAbort()
	Make/O test = NaN
	try
		CurveFit/N/Q line, test; AbortOnRTE
	catch
		if (V_AbortCode == -4)
			Print "Error during curve fit:"
			Variable cfError = GetRTError(1)	// 1 to clear the error
			Print GetErrMessage(cfError,3)
		endif
	endtry
End

If you run this function, the output is:

Error during curve fit:
You must have at least as many data points as fit parameters.

No error alert is presented because of the call to GetRTError. The error is reported to the user by getting the error message using GetErrMessage and then printing the message to the history area.

V_FitIterStart

V_FitIterStart provides a way for a user-defined function to know when the fitting routines are about to start a new iteration. The original, obsolete purpose of this is to allow for possible efficient computation of user-defined fit functions that involve convolution. Such functions should now use all-at-once fit functions. See All-At-Once Fitting Functions for details.

S_Info

If you create a string variable in a function that calls CurveFit or Funcfit, Igor will fill it with keyword-value pairs giving information about the fit:

Keyword	Information Following Keyword
DATE	The date of the fit.
TIME	The time of day of the fit.
FUNCTION	The name of the fitting function.
AUTODESTWAVE	If you used the /D parameter flag to request an autodestination wave, this keyword gives the name of the wave.
YDATA	The name of the Y data wave.
XDATA	A comma-separated list of X data waves, or "_calculated_" if there were no X waves. In most cases there is just one X wave.

Use StringByKey to get the information from the string. You should set keySepStr to "=" and listSepStr to ";".

Errors in Variables: Orthogonal Distance Regression

When you fit a model to data, it is usually assumed that all errors are in the dependent variable, and that independent variables are known perfectly (that is, X is set perfectly and Y is measured with error). This assumption is often not far from true, and as long as the errors in the dependent variable are much larger than those for the independent variable, it will not usually cause much difference to the curve fit.

When the errors are normally distributed with zero mean and constant variance, and the model is exact, then the standard least-squares fit gives the maximum-likelihood solution. This is the technique described earlier (see Overview of Curve Fitting).

In some cases, however, the errors in both dependent and independent variables may be comparable. This situation has a variety of names including errors in variables, measurement error models or random regressor models. An example of a model that can result in similar errors in dependent and independent variables is fitting the track of an object along a surface; the variables involved would be measurements of cartesian coordinates of the object's location at various instants in time. Presumably the measurement errors would be similar because both involve spatial measurement.

Fitting such data using standard or ordinary least squares can lead to bias in the solution. To solve this problem, we offer Orthogonal Distance Regression (ODR). Rather than minimizing the sum of squared errors in the dependent variable, ODR minimizes the orthogonal distance from the data to the fitted curve by adjusting both the model coefficients and an adjustment to the values of the independent variable. This is also sometimes called "total least squares" or "reduced major axis" regression (RMA) fitting.

For ODR curve fitting, Igor Pro uses a modified version of the freely available ODRPACK95. The CurveFit, FuncFit, and FuncFitMD operations can all do ODR fitting using the /ODR flag (see the documentation for the CurveFit operation for details on the /ODR flag, and the Curve Fitting References for information about the ODRPACK95 implementation of ODR fitting). Our version of ODRPACK95 has been modified to make it threadsafe and to do some automatic multithreading during single fits.

ODR Fitting is Threadsafe

As of Igor Pro 8.00, ODR fitting is threadsafe. You can perform an ODR fit from a threadsafe user-defined function and you can do multiple ODR fits simultaneously using Igor's preemptive threads.

Weighting Waves for ODR Fitting

Just as with ordinary least-squares fitting, you can provide a weighting wave to indicate the expected magnitude of errors for ODR fitting. But in ODR fitting, there are errors in both the dependent and independent variables, so ODR fits accept weighting waves for both. You use the /XW flag to specify weighting waves for the independent variable.

If you do not supply a weighting wave, it is assumed the errors have a variance of 1.0. This may be acceptable if the errors in the dependent and independent variables truly have similar magnitudes. But if the dependent and independent variables are of very different magnitudes, the chances are good that the errors are also of very different magnitudes, and weighting is essential for a proper fit. Unlike the case for ordinary least squares, where there is only a single weighting wave, ODR fitting depends on both the magnitude of the weights as well as the relative magnitudes of the X and Y weights.

ODR Initial Guesses

An ordinary least squares fit that is linear in the coefficients can be solved directly. No initial guess is required. The built-in line, poly, and poly2D curve fit functions are linear in the coefficients and do not require initial guesses.

An ordinary least-squares fit to a function that is nonlinear in the coefficients is an iterative process that requires a starting point. That means that you must provide an initial guess for the fit coefficients. The accuracy required of your initial guess depends greatly on the function you are fitting and the quality of your data. The built-in fit functions also attempt to calculate a good set of initial guesses, but for user-defined fits you must supply your own initial guesses.

An ODR fit introduces a nonlinearity into the fitting equations that requires iterative fitting and initial guesses even for fit functions that are linear in the fit coefficients. In the case of line, poly, and poly2D fit functions, ODR fitting uses an ordinary least squares fit to get an initial guess. For nonlinear built-in fit functions, the same initial guesses are used regardless of fitting method.

Because the independent variable is adjusted during the fit, an initial guess is also required for the adjustments to the independent variable. The initial guess is transmitted to Igor via one or more waves (one for each independent variable) specified with the /XR flag. The X residual wave is also an output- see ODR Fit Results.

In the absence of the /XR flag, initial guesses for the adjustments to the independent variable values are set to zero. This is usually appropriate; in areas where the fitting function is largely vertical, you may need nonzero guesses to fit successfully. One example of such a situation would be the region near a singularity.

Holding Independent Variable Adjustments

In some cases you may have reason to believe that you know some input values of the independent variables are exact (or nearly so) and should not be adjusted. To specify which values should not be adjusted, you supply X hold waves, one for each independent variable, via the /XHLD flag. These waves should be filled with zeroes corresponding to values that should be adjusted, or ones for values that should be held.

This is similar to the /H flag to hold fit coefficients at a set value during fitting. However, in the case of ODR fitting and the independent variable values, holds are specified by a wave instead of a string of ones and zeroes. This was done because of the potential for huge numbers of ones and zeroes being required. To save memory, you can use a byte wave for the holds. In the Make Waves dialog, you would select Byte 8 Bit from the Type menu. Use the /B flag with the Make operation.

ODR Fit Results

An ordinary least-squares fit involves adjusting the fit coefficients and calculating model values for the dependent variable. You can optionally have the fit calculate the residuals — the differences between the model and the dependent variable data.

ODR fitting adjusts both the fit coefficients and the independent variable values when seeking the least orthogonal distance fit. In addition to the residuals in the dependent variable, it can calculate and return to you a wave or waves containing the residuals in the independent variables, as well as a wave containing the adjusted values of the independent variable.

Residuals in the independent variable are returned via waves specified by the /XR flag. Note that the contents of these waves are inputs for initial guesses at the adjustments to the independent variables, so you must be careful — in most cases you will want to set the waves to zero before fitting.

The adjusted independent variable values are placed into waves you specify via the /XD flag.

Note that if you ask for an auto-destination wave (/D flag; see The Destination Wave) the result is a wave containing model values at a set of evenly-spaced values of the independent variables. This wave will also be generated in response to the /D flag for ODR fitting.

You can also specify a specific wave to receive the model values (/D=wave). The values are calculated at the values of the independent variables that you supply as input to the fit. In the case of ODR fitting, to make a graph of the model, the appropriate X wave would be the output from the /XD flag, not the input X values.

Constraints and ODR Fitting

When fitting with the ordinary least-squares method (/ODR=0) you can provide a text wave containing constraint expressions that will keep the fit coefficients within bounds. These expressions can be used to apply simple bound constraints (keeping the value of a fit coefficient greater than or less than some value) or to apply bounds on linear combinations of the fit coefficients (constrain a +b >1, for instance).

When fitting using ODR (/ODR=1 or more) only simple bound constraints are supported.

Error Estimates from ODR Fitting

In a curve fit, the output includes an estimate of the errors in the fit coefficients. These estimates are computed from the linearized quadratic approximation to the chi-square surface at the solution. For a linear fit (line, poly, and poly2D fit functions) done by ordinary least squares, the chi-square surface is actually quadratic and the estimates are exact if the measurement errors are normally distributed with zero mean and constant variance. If the fitting function is nonlinear in the fit coefficients, then the error estimates are an approximation. The quality of the approximation will depend on the nature of the nonlinearity.

In an ODR fit, even when the fitting function is linear in the coefficients, the fitting equations themselves introduce a nonlinearity. Consequently, the error estimates from an ODR fit are always an approximation. See the Curve Fitting References for detailed information.

ODR Fitting Examples

A simple example: a line fit with no weighting. If you run these commands, the call to SetRandomSeed will make your "measurement error" (provided by gnoise) the same as the example shown here:

SetRandomSeed 0.5                // so that the "random" data will always be the same...
Make/N=10 YLineData, YLineXData
YLineXData = p+gnoise(1)         // gnoise simulates error in X values
YLineData = p+gnoise(1)          // gnoise simulates error in Y values
// make a nice graph with errors bars showing standard deviation errors
Display YLineData vs YLineXData
ModifyGraph mode=3,marker=8
ErrorBars YLineData XY,const=1,const=1

Now we're ready to perform a line fit to the data. First, a standard curve fit:

CurveFit line, YLineData/X=YLineXData/D

This command results in the following history report:

fit_YLineData= W_coef[0]+W_coef[1]*x
W_coef={1.3711,0.78289}
V_chisq= 15.413; V_npnts= 10; V_numNaNs= 0; V_numINFs= 0; 
V_startRow= 0; V_endRow= 9; V_q= 1; V_Rab= -0.797202; V_Pr= 0.889708; 
V_r2= 0.791581;
W_sigma={0.727,0.142}
Coefficient values ± one standard deviation
	a = 1.3711 ± 0.727
	b = 0.78289 ± 0.142

Next, we will use /ODR=2 to request orthogonal distance fitting:

CurveFit/ODR=2 line, YLineData/X=YLineXData/D

which gives this result:

Fit converged properly
fit_YLineData= W_coef[0]+W_coef[1]*x
W_coef={1.0311,0.86618}
V_chisq= 9.18468; V_npnts= 10; V_numNaNs= 0; V_numINFs= 0; 
V_startRow= 0; V_endRow= 9; 
W_sigma={0.753,0.148}
Coefficient values ± one standard deviation
	a 	= 1.0311 ± 0.753
	b 	= 0.86618 ± 0.148

Add output of the X adjustments and Y residuals:

Duplicate/O YLineData, YLineDataXRes, YLineDataYRes
CurveFit/ODR=2 line, YLineData/X=YLineXData/D/XR=YLineDataXRes/R=YLineDataYRes

And a graph that uses error bars to show the residuals:

Display YLineData vs YLineXData
ModifyGraph mode=3,marker=8
AppendToGraph fit_YLineData
ModifyGraph rgb(YLineData)=(0,0,65535)
ErrorBars YLineData BOX,wave=(YLineDataXRes,YLineDataXRes),wave=(YLineDataYRes,YLineDataYRes)

The boxes on this graph do not show error estimates, they show the residuals from the fit. That is, the differences between the data and the fit model. Because this is an ODR fit, there are residuals in both X and Y; error bars are the most convenient way to show this. Note that one corner of each box touches the model line.

In the next example, we do an exponential fit in which the Y values and errors are small compared to the X values and errors. The curve fit history report has been edited to include just the output of the solution. First, fake data and a graph:

SetRandomSeed 0.5	// so that the "random" data will always be the same...
Make/D/O/N=20 expYdata, expXdata
expYdata = 1e-6*exp(-p/2)+gnoise(1e-7)
expXdata = p+gnoise(1)
Display expYdata vs expXdata
ModifyGraph mode=3,marker=8

A regular exponential fit:

CurveFit exp, expYdata/X=expXdata/D

Coefficient values ± one standard deviation
  	y0    	=-1.0805e-08 ± 4.04e-08
  	A     	=7.0438e-07 ± 9.37e-08
  	invTau	=0.38692 ± 0.116

An ODR fit with no weighting, with X and Y residuals:

Duplicate/O expYdata, expYdataResY, expYdataResX
expYdataResY=0
expYdataResX=0
CurveFit/ODR=2 exp, expYdata/X=expXdata/D/R=expYdataResY/XR=expYdataResX

Coefficient values ± one standard deviation
	y0    	=-1.0541e-08 ± 4.03e-08
  	A     	=7.0443e-07 ± 9.37e-08
  	invTau	=0.38832 ± 0.116

And a graph:

Display /W=(137,197,532,405) expYdata vs expXdata
AppendToGraph fit_expYdata
ModifyGraph mode(expYdata)=3
ModifyGraph marker(expYdata)=8
ModifyGraph lSize(expYdata)=2
ModifyGraph rgb(expYdata)=(0,0,65535)
ErrorBars expYdata BOX,wave=(expYdataResX,expYdataResX),wave=(expYdataResY,expYdataResY)

Because the Y values are very small compared to the X values, and we didn't use weighting to reflect smaller errors in Y, the residual boxes are tall and skinny. If the vertical graph scale were the same as the horizontal scale, the boxes would be approximately square. The data line would be very nearly a horizonal line. One way to understand this is to remember that the ODR method is essentially geometric. In this example, the vertical scale on the graph has been expanded very greatly, but the ODR method works in an unexpanded scale where the perpendicular lines to the fit curve are very nearly exactly vertical.

Now we can add appropriate weighting. t's easy to decide on the correct weighting since we added "measurement error" using gnoise():

Duplicate/O expYdata, expYdataWY
expYdataWY=1e-7
Duplicate/O expYdata, expYdataWX
expYdataWX=1
CurveFit/ODR=2 exp, expYdata/X=expXdata/D/R=expYdataResY/XR=expYdataResX/W=expYdataWY/XW=expYdataWX/I=1

Coefficient values ± one standard deviation
	y0    	=-9.8498e-09 ± 3e-08
  	A     	=1.0859e-06 ± 5.39e-07
  	invTau	=0.57731 ± 0.248

One way to think about the weighting waves for ODR fitting is that they provide geometric scaling. In this example, the vertical dimension is about 10⁷ times smaller than the horizontal dimension. When the vertical dimension is scaled by the weighting waves, the dimensions are similar and the perpendicular distances from the fit curve to the data points are no longer merely vertical.

Fitting Implicit Functions

Occasionally you may need to fit data to a model that doesn't have a form that can be expressed as y = f(x). An example would be fitting a circle or ellipse using an equation like

\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1

Because this equation can't be expressed as y = f(x), you can't write a standard user-defined fitting function for it.

This problem is related to the errors in variables problem in which data has measurement errors in both the dependent and independent variables. You have two inputs, or independent variables (x and y), both with (probably) similar measurement errors. It differs from errors in variables fitting in that the function output is zero instead of being a dependent variable.

The ODRPACK95 package also supports fitting to implicit functions, which you can do with the /ODR=3 flag. You create a fitting function with multiple independent variables (in the case of the ellipse above, two for x and y). The fitting process will attempt to find x and y residuals and fit coefficients to minimize the distance from the data to the zero contour of the function.

It may be a good idea at this point to read the section about errors in variables fitting; see Errors in Variables: Orthogonal Distance Regression; much of it applies also to implicit fits.

There are a few differences between regular fitting and implicit fitting. For implicit fits, there is no autodestination, and the report printed in the history does not include the wave assignment showing how to get values of the fitted model (doing that is actually not at all easy).

Because of the details of the way ODRPACK95 operates, when you do an implicit fit, the curve fit progress window does not update, and it appears that the fit takes just one iteration. That is because all the action takes place inside the call to ODRPACK95.

The fit function must be written to return zero when the function solution is found. So if you have an equation of the form f(x_i) = 0, you are ready to go; you simply create a fit function that implements f(x_i). If it is in the form f(x_i) = constant, you must move the constant to the other side of the equation: f(x_i)-constant = 0. If it is a form like f(x_i) = g(x_i), you must write your fitting function to return f(x_i) - g(x_i).

Example: Fit to an Ellipse

In this example we will show how to fit an equation like the one above. In the example the center of the ellipse will be allowed to be at non-zero x₀, y₀.

First, we must define a fitting function. The function includes special comments to get mnemonic names for the fit coefficients (see The New Fit Function Dialog Adds Special Comments). To try the example, you will need to copy this function and paste it into the Procedure window:

Function FitEllipse(w,x,y) : FitFunc
	Wave w
	Variable x
	Variable y

	//CurveFitDialog/
	//CurveFitDialog/ Coefficients 4
	//CurveFitDialog/ w[0] = a
	//CurveFitDialog/ w[1] = b
	//CurveFitDialog/ w[2] = x0
	//CurveFitDialog/ w[3] = y0

	return ((x-w[2])/w[0])^2 + ((y-w[3])/w[1])^2 - 1
End

To do an implicit fit, Igor seeks adjustments to the input data and fit coefficients that cause the fit function to return zero. To implement the ellipse function above, it is necessary to subtract 1.0 to account for "= 1" on the right in the equation above.

The hard part of creating an example is creating fake data that falls on an ellipse. We will use the standard parametric equations to do the job (y = acos(theta), x=bsin(theta)). So far, we will not add "measurement error" to the data so that you can see the ellipse clearly on a graph:

Make/N=20 theta,ellipseY,ellipseX
theta = 2*pi*p/20
ellipseY = 2*cos(theta)+2
ellipseX=3*sin(theta)+1

A graph of the data (you could use the Windows→New Graph menu, and then the Modify Trace Appearance dialog):

Display ellipseY vs ellipseX
ModifyGraph mode=3,marker=8
ModifyGraph width={perUnit,72,bottom},height={perUnit,72,left}

The last command line sets the width and height modes of the graph so that the ellipse is shown in its true aspect ratio. Now add some "measurement error" to the data:

SetRandomSeed 0.5	// so that the "random" data will always be the same...
ellipseY += gnoise(.3)
ellipseX += gnoise(.3)

Now you can see why we didn't do that before — it's a pretty lousy ellipse!

Now, finally, do the fit. That requires making a coefficient wave and filling it with the initial guesses, and making a pair of waves to receive estimated values of X and Y at the fit:

Duplicate ellipseY, ellipseYFit, ellipseXFit
Make/D/O ellipseCoefs={3,2,1,2}			// a, b, x0, y0
FuncFit/ODR=3 FitEllipse, ellipseCoefs /X={ellipseX, ellipseY}/XD={ellipseXFit,ellipseYFit}

The call to the FuncFit operation has no Y wave specified (it would ordinarily go right after the coefficient wave, ellipseCoefs) because this is an implicit fit.

The results:

Fit converged properly
ellipseCoefs={3.1398,1.9045,0.92088,1.9971}
V_chisq= 1.74088; V_npnts= 20; V_numNaNs= 0; V_numINFs= 0; 
W_sigma={0.158,0.118,0.128,0.0906}
Coefficient values ± one standard deviation
  	a 	=3.1398 ± 0.158
  	b 	=1.9045 ± 0.118
  	x0	=0.92088 ± 0.128
  	y0	=1.9971 ± 0.0906

And add the destination waves (the ones specified with the /XD flag) to the graph:

AppendToGraph ellipseYFit vs ellipseXFit
ModifyGraph mode=3,marker(ellipseYFit)=1
ModifyGraph rgb=(1,4,52428)

It is difficult to compute the model representing the solution, as it requires finding roots of the implicit function. A quick way to add a smooth model curve to a graph is to fill a matrix with values of the fit function at a range of X and Y and then add a contour plot of the matrix to your graph. Then modify the contour plot to show only the zero contour.

Here are commands to add a contour of the example function to the graph above:

Make/N=(100,100) ellipseContour
SetScale/I x -3,4.5,ellipseContour
SetScale/I y -.2, 5, ellipseContour
ellipseContour = FitEllipse(ellipseCoefs, x, y)
AppendMatrixContour ellipseContour
ModifyContour ellipseContour labels=0,autoLevels={*,*,0},moreLevels=0,moreLevels={0}
ModifyContour ellipseContour rgbLines=(0,0,0)

And the resulting graph:

Fitting Sums of Fit Functions

Sometimes the appropriate model is a combination, typically a sum, of simpler models. It might be a sum of exponential decay functions, or a sum of several different peaks at various locations. Peak fitting can include a baseline function implemented as a separate user-defined fit function. With standard curve fitting, you have to write a user-defined function that implements the sum.

Instead, you can use an alternate syntax for the FuncFit operation to fit to a list of fit functions that are summed automatically. The results for each fit function are returned via separate coefficient waves, making it easy to keep the results of each term in the sum separate. The syntax is described in the reference documentation for the FuncFit operation.

The sum-of-fit-functions feature can mix any kind of fit function — built-in, or any of the variants described in User-Defined Fitting Functions. However, even if you use only built-in fit functions you must provide initial guesses because our initial-guess generating code cannot discern how the various features of the data are partitioned amongst the list of fit functions.

Linear Dependency: A Major Issue

When you fit a list of fit functions you must be careful not to introduce linear dependencies between the coefficients of the list of functions. The most likely such dependency will arise from a constant Y offset used with all of the built-in fit functions, and commonly included in user functions. This Y offset accounts for any offset error that is common when making real-world measurements. For instance, the equation for the built-in exp function is:

\displaystyle y_{0}+A \exp (-B x)

If you sum two terms, you get two y₀'s (primes used for the second copy of the function):

\displaystyle y_{0}+A \exp (-B x)+y_{0}^{\prime}+A^{\prime} \exp \left(-B^{\prime} x\right)

As long as B and B' are distinct, the two exponential terms will not be a problem. But y₀ and y'₀ are linearly dependent — they cannot be distinguished mathematically. If you increase one and decrease the other the same amount, the result is exactly the same. This is sure to cause a singular matrix error when you try to do the fit.

The solution is to hold one of the y₀ coefficients. Because each fit function in the list has its own coefficient wave, and you can specify a hold string for each function, this is easy (see the first example below).

There are many ways to introduce linear dependence. They are not always so easy to spot!

Constraints Applied to Sums of Fit Functions

The sums of fit functions feature does not include a keyword for specifying constraints on a function-by-function basis. But you can use the normal constraint specifications - you just have to translate the constraint expressions to take account of the list of functions. (If you are interested in using constraints, but don't know about the syntax for constraints, see Fitting With Constraints.)

Constraint expressions use Kn to designate fit coefficients where n is simply the sequential number of the fit coefficient within the list of coefficients. n starts with zero. In order to reference fit coefficients for a fit function in a list of summed fit functions, you must account for all the fit coefficients in all the fit functions in the list before the fit function you are trying to constrain. For example, this is part of a command that will fit a sum of three exponential terms:

FuncFit {{exp, expTerm1},{exp, expTerm2, hold="1"},{exp, expTerm3, hold="1"}} ...

In order to constrain coefficients of the second exponential term, you must know first that the built-in exp fit function has three fit coefficients. Here is the equation of the exp fit function:

f(x) = y0 + A*exp(-x*invTau)

The vertical offset (y0) of the first summed exp term is represented in a constraint expression as "K0", the amplitude as "K1", and invTau as "K2". Constraint expressions for the second exp term continue the count starting with "K3" for y0 (but see the section Linear Dependency: A Major Issue and note that you are not allowed to hold and constrain a fit coefficient simultaneously), and use "K4" for the amplitude and "K5" for invTau.

Example: Summed Exponentials

This example fits a sum of three exponentials using the built-in exp fit function. For real work, we recommend the exp_XOffset function; it handles data that's not at X=0 better, and the decay constant fit coefficient is actually the decay constant. The exp fit function gives you the inverse of the decay constant.

First, make some fake data and graph it:

Make/D/N=1000 expSumData
SetScale/I x 0,1,expSumData
expSumData = 1 + exp(-x/0.5) + 1.5*exp(-x/.1) + 2*exp(-x/.01)+gnoise(.03)
Display expSumData
ModifyGraph mode=2,rgb=(1,4,52428)

The fake data was purposely made with a Y offset of 1.0 in order to illustrate how to handle the vertical offset terms in the fit function.

Next, we need to make a coefficient wave for each of the fit functions. In spite of the linear dependence between the vertical offset in each copy of the function, you must include all the fit coefficients in the coefficient waves. Otherwise when the function is evaluated the fit won't have all the needed information.

Make/D/O expTerm1 = {1, 1, 2}
Make/D/O expTerm2 = {0, 1.5, 10}
Make/D/O expTerm3 = {0, 2, 100}

Each of these lines makes one coefficient wave with three elements. The first element is y₀, the second is amplitude, and the third is the inverse of the decay constant. Since the data is fake, we have a pretty good idea of the initial guesses!

To reflect the baseline offset of 1.0, the y₀ coefficient for only the first exponential coefficient wave was set to 1. If y₀ were set to 1.0 for all three, the offset would be 3.0.

Now we can do the fit. A FuncFit command with a list of fit functions and coefficient waves can be pretty long:

FuncFit {{exp, expTerm1},{exp, expTerm2, hold="1"},{exp, expTerm3, hold="1"}} expSumData/D

The entire list of functions is enclosed in braces and each fit function specification in the list is enclosed in braces as well. At a minimum you must provide a fit function and a coefficient wave for each function in the list, as was done here for the first exponential term.

The specification for each function can also contain various keywords; the second and third terms here contain the hold keyword in order to include a hold string. The string used will cause the fit to hold the y₀ coefficient for the second and third terms at zero. That prevents problems caused by linear dependence between the three fit functions. Since the coefficient waves for the second and third terms set their respective y₀ to zero, this puts all the vertical offset into the one coefficient for the first term.

In this example the hold strings are literal quoted strings. They can be any string expression but see below for restrictions if you use a function list contained in a string:

String holdStr = "1"
FuncFit {{exp,expTerm1},{exp,expTerm2,hold=holdStr},{exp,expTerm3,hold="1"}} expSumData/D

The history report for a sum of fit functions is enhanced to show all the functions:

Fit converged properly
fit_expSumData= Sum of Functions(,x)
expTerm1={1.027,1.045,2.2288}
expTerm2={0,1.4446,10.416}
expTerm3={0,2.0156,102.28}
V_chisq= 0.864844; V_npnts= 1000; V_numNaNs= 0; V_numINFs= 0; 
V_startRow= 0; V_endRow= 999; V_startCol= 0; V_endCol= 0; 
V_startLayer= 0; V_endLayer= 0; V_startChunk= 0; V_endChunk= 0; 
W_sigma={0.0184,0.0484,0.185,0,0.052,0.495,0,0.0239,2.34}
For function 1: exp:
Coefficient values ± one standard deviation
	y0     	= 1.027 ± 0.0184
	A      	= 1.045 ± 0.0484
	invTau 	= 2.2288 ± 0.185
For function 2: exp:
Coefficient values ± one standard deviation
	y0     	= 0 ± 0
	A      	= 1.4446 ± 0.052
	invTau 	= 10.416 ± 0.495
For function 3: exp:
Coefficient values ± one standard deviation
	y0     	= 0 ± 0
	A      	= 2.0156 ± 0.0239
invTau 	= 102.28 ± 2.34

Example: Function List in a String

The list of functions in the FuncFit command in the first example is moderately long, but it could be much longer. If you wanted to sum 20 peak functions and a baseline function, the list could easily exceed the limit of 2500 bytes in a command line.

Fortunately, you can build the function specification in a string variable and use the string keyword. Doing this on the command line for the first example looks like this:

String myFunctions="{exp, expTerm1}"
myFunctions+="{exp, expTerm2, hold=\"1\"}"
myFunctions+="{exp, expTerm3, hold=\"1\"}"
FuncFit {string = myFunctions} expSumData/D

These commands build the list of functions one function specification at a time. The second and third lines use the += assignment operator to add additional functions to the list. Each function specification includes its pair of braces.

Notice the treatment of the hold strings — in order to include quotation marks in a quoted string expression, you must escape the quotation marks. Otherwise the command line parser thinks that the first quote around the hold string is the closing quote.

The function list string is parsed at run-time outside the context in which FuncFit is running. Consequently, you cannot reference local variables in a user-defined function. The hold string may be either a quoted literal string, as shown here, or it can be a reference to a global variable, including the full data folder path:

String/G root:myDataFolder:holdStr="1"
String myFunctions="{exp, expTerm1}"
myFunctions+="{exp, expTerm2, hold=root:myDataFolder:holdStr}"
myFunctions+="{exp, expTerm3, hold=root:myDataFolder:holdStr}"
FuncFit {string = myFunctions} expSumData/D

Fitting with Complex-Valued Functions

Prior to Igor Pro 9.00, to fit complex-valued functions to complex-valued data required writing a real-valued fit function that used a special organization of the data to pack real and imaginary parts into a single real-valued wave. Now Igor supports fitting to complex-valued fitting functions directly.

The basic requirement for fitting complex-valued functions is to write a fit function that returns a complex result. Igor supports the traditional format for a user-defined fit function (see Format of a Basic Fitting Function) and all-at-once format (All-At-Once Fitting Functions), but the return type of a basic fit function or the Y wave in an all-at-once fit function must be complex. Complex fitting functions are not supported by structure fit functions or by the sum-of-fit-functions format.

No Dialog Support for Complex Fitting

The Curve Fitting dialog does not allow you to select complex waves, or fit functions that return complex values. It may be possible to use a real-valued function and waves to set up a fit in the dialog, then click the To Cmd Line button to copy the generated command to the command line where you can edit the command. It's probably easier to read the reference documentation for the FuncFit operation and simply compose a command.

Complex Basic Fitting Function

The basic format for a complex-valued function looks like this:

Function/C F(Wave w, Variable xx) : FitFunc
	<body of function>
	<return statement>
End

The /C in "Function/C" tells Igor that the function returns a complex value. As shown above, the function takes a real-valued coefficient wave and a real-valued independent variable. If your particular function needs the coefficient wave and/or independent variable to be complex-valued, add /C to the parameter declaration:

Function/C F(Wave/C w, Variable/C xx) : FitFunc
	<body of function>
	<return statement>
End

We show here both the coefficient wave and the independent variable being complex; either one or both can be complex.

If you specify a complex independent variable, then you must supply a complex-valued X wave. Since Igor's wave scaling cannot be complex, if your fitting function requires a complex independent variable then you must have a separate X wave as input to the FuncFit operation.

Complex Basic Multivariate Fitting Function

As with normal real-valued fitting functions, you can write multivariate fitting functions that return complex values:

Function/C F(Wave w, Variable x1, Variable x2) : FitFunc
	<body of function>
	<return statement>
End

As before, the coefficient wave can be either real or complex, and the independent variables can be real or complex. The independent variables must be either all real-valued or all complex-valued.

Complex All-At-Once Fitting Function

In certain cases, a fit function may need to produce all model values at one time. You can write an all-at-once fitting functions that implement complex-valued functions:

Function AAOFitFunc(Wave pw, Wave/C yw, Wave xw) : FitFunc
	yw = <expression involving pw and xw>
End

Unlike the basic format, the function does not return a complex value and is not declared with Function/C. Instead, the all-at-once fit function returns the complex model values to Igor via the yw wave which you must declare as complex using /C.

As with the basic format, you can make the coefficient wave pw complex or real, and you can make the independent variable wave xw complex or real, as long as the type matches the waves you pass to the FuncFit operation.

All-at-once fitting functions can be multivariate functions, too, by adding more x input waves. As with the basic format, independent variable inputs must be all either real or complex.

Other Waves

A variety of other waves may be used during a fit: weighting, masking, epsilon, and residuals waves, and a destination wave to receive the model values of the fit solution. All of these waves must be complex or real depending on the nature of the fitting function.

Weighting applied to the dependent variable values must always be complex because a complex fitting function by definition returns complex dependent variable values. Residual and destination waves must be complex for the same reason.

If you use an epsilon wave, it must match your coefficient wave.

Mask waves must be real; they select data points, and cannot select just the real or imaginary part of your input data.

If you are fitting with errors in both dependent and independent variables, the X weighting waves must match the type of your independent variable inputs.

Curve Fitting with Multiple Processors

If you are using a computer with multiple processors, you no doubt want to take advantage of them. Curve fitting can take advantage of multiple processors in two ways:

Automatic multithreading
Programmed multithreading

Curve Fitting with Automatic Multithreading

If you use the built-in fit functions or thread-safe user-defined fit functions in the basic or all-at-once formats, Igor automatically uses multiple processors if your data set is "large enough". The number of points required to be "large enough" is set by the MultiThreadingControl operation.

There are two keywords used by MultiThreadingControl for curve fitting. The CurveFit1 keyword controls automatic multithreading with built-in and basic format user-defined fit functions. The CurveFitAllAtOnce keyword controls automatic multithreading with user-defined fit functions in the all-at-once format. The appropriate setting of these limits depends on the complexity of the fitting function and the nature of your problem. It can be best determined only by experimentation.

The automatic multithreading added in Igor 7 makes the CurveFit /NTHR flag obsolete. The automatic multithreading is more effective than the threading available in Igor 6.

Automatic multithreading when doing ODR fits (see Errors in Variables: Orthogonal Distance Regression) is most effective with fit functions having large numbers of fit coefficients and with user-defined fit functions that are expensive to compute. Surprisingly, it may be more effective with fewer input data points.

If you use the Threadsafe keyword with your user-defined fit function and Igor's automatic multithreading is enabled for your fit, your function must not access waves or global variables. Therefore your function must not use WAVE, NVAR or SVAR declarations.

Curve Fitting with Programmed Multithreading

The CurveFit, FuncFit, and FuncFitMD operations are threadsafe. Consequently another way to use multiple processors is to do more than one curve fit simultaneously, with each fit using a different processor. This requires threadsafe programming, as described under ThreadSafe Functions and Multitasking, and requires at least intermediate-level Igor programming skills.

The fitting function can be either a built-in fit function or a threadsafe user-defined fit function.

For an example, choose File→Example Experiments→Curve Fitting→MultipleFitsInThreads.

Constraints and ThreadSafe Functions

The usual way to specify constraints to a curve fit is via expressions in a text wave (see Fitting with Constraints). As part of the process of parsing these expressions and getting ready to use them in a curve fit involves evaluating part of the expressions. That, in turn, requires sending them to Igor's command-line interpreter, in a process very similar to the way the Execute operation works. Unfortunately, this is not threadsafe.

Instead, you must use the method described in Constraint Matrix and Vector. Unfortunately, it is hard to understand, inconvenient to set up, and easy to make mistakes. The best way to do it is to set up your constraint expressions using the normal text wave method (see Constraint Expressions) and use the /C flag with a trial fit. Igor will generate the matrix and vector required.

In most cases, the basic expressions will not change from one fit to another, just the limits of the constraints will change. If that is the case, you can use the matrix provided by Igor, and alter the numbers in the vector to change the constraint limits.

Multithreading Demo

Open Multiple Fits In Threads Demo

User-Defined Fitting Functions

When you use the New Fit Function dialog to create a user-defined function, the dialog uses the information you enter to create code for your function in the Procedure window. Using the New Fit Function dialog is the easiest way to create a user-defined fitting function, but it is possible also to write the function directly in the Procedure window.

Certain kinds of complexities will require that you write the function yourself. It may be that the easiest way to create such a function is to create a skeleton of the function using the dialog, and then modify it by editing in the procedure window.

This section describes the format of user-defined fitting functions so that you can understand the output of the New Fit Function dialog, and so that you can write one yourself.

You can use a variety of formats for user-defined fit functions tailored to different situations, and involving varying degrees of complexity to write and use. The following section describes the simplest format, which is also the format created by the New Fit Function dialog.

User-Defined Fit Function Formats

You can use three formats for user-defined fitting functions: the Basic format discussed above, the All-At-Once format, and Structure Fit Functions, which use a structure as the only input parameter. Additionally, Structure Fit Functions come in basic and all-at-once variants. Each of these formats address particular situations.

The basic format (see Format of a Basic Fitting Function) was the original format. It returns just one model value at a time.

The all-at-once format (see All-At-Once Fitting Functions) addresses problems in which the operations involved, such as convolution, integration, or FFT, naturally calculate all the model values at once. Because of reduced function-call overhead, it is somewhat faster than the basic format for large data sets.

The structure-based format (see Structure Fit Functions) uses a structure as the only function parameter, allowing arbitrary information to be transmitted to the function during fitting. This makes it very flexible, but also makes it necessary that FuncFit be called from a user-defined function.

Format of a Basic Fitting Function

A basic user-defined fitting function has the following form:

Function F(w, x) : FitFunc
	WAVE w; Variable x

	<body of function>
	<return statement>
End

You can choose a more descriptive name for your function, of course.

The function must have exactly two parameters in the univariate case shown above. The first parameter is the coefficients wave, conventionally called w. The second parameter is the independent variable, conventionally called x. If your function has this form, it will be recognized as a curve fitting function and will allow you to use it with the FuncFit operation.

The FitFunc keyword marks the function as being intended for curve fitting. Functions with the FitFunc keyword that have the correct format are included in the Function menu in the Curve Fitting dialog.

The FitFunc keyword is not required. The FuncFit operation will allow any function that has a wave and a variable as the parameters. In the Curve Fitting dialog you can select Show Old-Style Functions from the Function menu in order to display a function that lacks the FitFunc keyword, but you may also see functions that just happen to match the correct format but aren't fitting functions.

Note that the function does not know anything about curve fitting. All it knows is how to compute a return value from its input parameters. The function is called during a curve fit when it needs the value for a certain X and a certain set of fit coefficients.

Here is an example of a user-defined function to fit a log function. This might be useful since log is not one of the functions provided as a built-in fit function.

Function LogFit(w,x) : FitFunc
	WAVE w
	Variable x

	return w[0]+w[1]*log(x)
End

In this example, two fit coefficients are used. Note that the first is in the zero element of the coefficient wave. You cannot leave out an index of the coefficient wave. Igor uses the size of your coefficient wave to determine how many coefficients need to be fit. Consequently an unused element of the wave results in a singular matrix error.

Intermediate Results for Very Long Expressions

The body of the function is usually fairly simple but can be arbitrarily complex. If necessary, you can use local variables to build up the result, piece-by-piece. You can also call other functions or operations and use loops and conditionals.

If your function has many terms, you might find it convenient to use a local variable to store intermediate results rather than trying to put the entire function on one line. For example, instead of:

return w[0] + w[1]*x + w[2]*x^2

you could write:

Variable val	// local variable to accumulate result value
val = w[0]
val += w[1]*x
val += w[2]*x^2
return val

We often get fitting functions from our customers that use extremely long expressions derived by Mathematica. These expressions are hard to read and understand, and highly resistant to debugging and modification. It is well worth some effort to break them down using assignments to intermediate results.

Conditionals

Flow control statements including "if" statements are allowed in fit functions. You could use this to fit a piece-wise function, or to control the return value in the case of a singularity in the function.

Here is an example of a function that fits two lines to different sections of the data. It uses one of the parameters to decide where to switch from one line to the other:

Function PieceWiseLineFit(w,x) : FitFunc
	WAVE w
	Variable x

	Variable result
	if (x < w[4])
		result = w[0]+w[1]*x
	else
		result = w[2]+w[3]*x
	endif
	return result
End

This function can be entered into the New Fit Function dialog. Here is what the dialog looked like when we created the function above:

The New Fit Function Dialog Adds Special Comments

In the example above of a piece-wise linear fit function, the New Fit Function dialog uses coefficient names instead of indexing a coefficient wave, but there isn't any way to name coefficients in a fit function. The New Fit Function dialog adds special comments to a fit function that contain extra information. For instance, the PieceWiseLineFit function as created by the dialog looks like this:

Function PieceWiseLineFit(w,x) : FitFunc
	WAVE w
	Variable x

	//CurveFitDialog/ These comments were created by the Curve Fitting dialog. Alteri
	//CurveFitDialog/ make the function less convenient to work with in the Curve Fit
	//CurveFitDialog/ Equation:
	//CurveFitDialog/ variable result
	//CurveFitDialog/ if (x < breakX)
	//CurveFitDialog/  result = a1+b1*x
	//CurveFitDialog/ else
	//CurveFitDialog/  result = a2+b2*x
	//CurveFitDialog/ endif
	//CurveFitDialog/ f(x) = result
	//CurveFitDialog/ End of Equation
	//CurveFitDialog/ Independent Variables 1
	//CurveFitDialog/ x
	//CurveFitDialog/ Coefficients 5
	//CurveFitDialog/ w[0] = a1
	//CurveFitDialog/ w[1] = b1
	//CurveFitDialog/ w[2] = a2
	//CurveFitDialog/ w[3] = b2
	//CurveFitDialog/ w[4] = breakX

	Variable result
	if (x < w[4])
		result = w[0]+w[1]*x
	else
		result = w[2]+w[3]*x
	endif
	return result
End

If you click the Edit Fit Function button, the function code is analyzed to determine the number of coefficients. If the comments that name the coefficients are present, the dialog uses those names. If they are not present, the coefficient wave name is used with the index number appended to it as the coefficient name.

Having mnemonic names for the fit coefficients is very helpful when you look at the curve fit report in the history area. The minimum set of comments required to have names appear in the dialog and in the history is a lead-in comment line, plus the Coefficients comment lines. For instance, the following version of the function above will allow the Curve Fitting dialog and history report to use coefficient names:

Function PieceWiseLineFit(w,x) : FitFunc
	WAVE w
	Variable x

	//CurveFitDialog/
	//CurveFitDialog/ Coefficients 5
	//CurveFitDialog/ w[0] = a1
	//CurveFitDialog/ w[1] = b1
	//CurveFitDialog/ w[2] = a2
	//CurveFitDialog/ w[3] = b2
	//CurveFitDialog/ w[4] = breakX

	variable result
	if (x < w[4])
	 result = w[0]+w[1]*x
	else
	 result = w[2]+w[3]*x
	endif
	return result
End

The blank comment before the line with the number of coefficients on it is required- the parser that looks at these comments needs one lead-in line to throw away. That line can contain anything as long as it includes the lead-in "//CurveFitDialog/".

Functions that the Fit Function Dialog Doesn't Handle Well

In the example functions it is quite clear by looking at the function code how many fit coefficients a function requires, because the coefficients wave is indexed with a literal number. The number of coefficients is simply one more than the largest index used in the function.

Occasionally a fit function uses constructions other than a literal number for indexing the coefficient wave. This will make it impossible for the Curve Fitting dialog to figure out how many coefficients are required. In this case, the Coefficients tab can't be constructed until you tell the dialog how many coefficients are needed. You do this by choosing a coefficient wave having the right number of points from the Coefficient Wave menu.

You cannot edit such a function by clicking the Edit Fit Function button. You must write and edit the function in the Procedure window.

Here is an example function that can fit an arbitrary number of Gaussian peaks. It uses the length of the coefficient wave to determine how many peaks are to be fit. Consequently, it uses a variable rather than a literal number to access the coefficients:

Function FitManyGaussian(w, x) : FitFunc
	WAVE w
	Variable x

	Variable returnValue = w[0]
	Variable i
	Variable numPeaks = floor((numpnts(w)-1)/3)
	Variable cfi

	for (i = 0; i < numPeaks; i += 1)
		cfi = 3*i+1
		returnValue += w[cfi]*exp(-((x-w[cfi+1])/w[cfi+2])^2)
	endfor
	return returnValue
End

Format of a Multivariate Fitting Function

A multivariate fitting function has the same form as a univariate function, but has more than one independent variable:

Function F(w, x1, x2, ...) : FitFunc
	WAVE w;
	Variable x1
	Variable x2
	Variable ...

	<body of function>
	<return statement>
End

A function to fit a planar trend to a data set could look like this:

Function Plane(w, x1, x2) : FitFunc
	WAVE w
	Variable x1, x2

	return w[0] + w[1]*x1 + w[2]*x2
End

There is no limit on the number of independent variables, with the exception that the entire Function declaration line must fit within a single command line of 2500 bytes.

The New Fit Function dialog will add the same comments to a multivariate fit function as it does to a basic fit function. The Plane() function above might look like this (we have truncated the first two special comment lines to make them fit):

Function Plane(w,x1,x2) : FitFunc
	WAVE w
	Variable x1
	Variable x2

	//CurveFitDialog/ These comments were created by the Curve... 
	//CurveFitDialog/ make the function less convenient to work...
	//CurveFitDialog/ Equation:
	//CurveFitDialog/ f(x1,x2) = A + B*x1 + C*x2
	//CurveFitDialog/ End of Equation
	//CurveFitDialog/ Independent Variables 2
	//CurveFitDialog/ x1
	//CurveFitDialog/ x2
	//CurveFitDialog/ Coefficients 3
	//CurveFitDialog/ w[0] = A
	//CurveFitDialog/ w[1] = B
	//CurveFitDialog/ w[2] = C

	return w[0] + w[1]*x1 + w[2]*x2
End

All-At-Once Fitting Functions

The scheme of calculating one Y value at a time doesn't work well for some fitting functions. This is true of functions that involve a convolution such as might arise if you are trying to fit a theoretical signal convolved with an instrument response. Fitting to a solution to a differential equation might be another example.

For this case, you can create an "all at once" fit function. Such a function provides you with an X and Y wave. The X wave is input to the function; it contains all the X values for which your function must calculate Y values. The Y wave is for output — you put all your Y values into the Y wave.

Because an all-at-once function is called only once for a given set of fit coefficients, it will be called many fewer times than a basic fit function. Because of the saving in function-call overhead, all-at-once functions can be faster even for problems that don't require an all-at-once function.

Here is the format of an all-at-once fit function:

Function myFitFunc(pw, yw, xw) : FitFunc
	WAVE pw, yw, xw

	yw = <expression involving pw and xw>
End

Note that there is no return statement because the function result is put into the wave yw. Even if you include a return statement the return value is ignored during a curve fit.

The X wave contains all the X values for your fit, whether you provided an X wave to the curve fit or not. If you did not provide an X wave, xw simply contains equally-spaced values derived from your Y wave's X scaling.

There are some restrictions on all-at-once fitting functions:

You can't create or edit an all-at-once function using the Curve Fitting dialog. You must create it by editing in the Procedure window. All-at-once functions are, however, listed in the Function menu in the Curve Fitting dialog.
There is no such thing as an "old-style" all-at-once function. It must have the FitFunc keyword.
You don't get mnemonic coefficient names.

Here is an example that fits an exponential decay using an all-at-once function. This example is silly — there is no reason to make this an all-at-once function. It is simply an example showing how a real function works without the computational complexities. Here it is, as an all-at-once function:

Function allatonce(pw, yw, xw) : FitFunc
	WAVE pw, yw, xw

	// a wave assignment does the work
	yw = pw[0] + pw[1]*exp(-xw/pw[2])
End

This is the same function written as a standard user fitting function:

Function notallatonce(pw, x) : FitFunc
	WAVE pw
	Variable x

	return pw[0] + pw[1]*exp(-x/pw[2])
End

Note that in the all-at-once function, the argument of exp() includes xw, a wave. The basic format uses the input parameter x, which is a variable containing a single value. The use of xw in the all-at-once version of the function uses the implied point number feature of wave assignments (see Waveform Arithmetic and Assignment).

There are some things to watch out for when creating an all-at-once fitting function:

You must not change the yw wave except for assigning values to it. You must not resize it. This will get you into trouble:

	Function allatonce(pw, yw, xw) : FitFunc
		WAVE pw, yw, xw

		Redimension/N=2000 yw	// BAD!
		yw = pw[0] + pw[1]*exp(-xw/pw[2])
	End

You may not get the same number of points in yw and xw as you have in the waves you provide as the input data. If you fit to a restricted range, if there are NaN's in the input data, or if you use a mask wave to select a subset of the input data, you will get a wave with a reduced number of points. Your fitting function must be written to handle that situation or you must not use those features.
It is tricky, but not impossible, to write an all-at-once fitting function that works correctly with the auto-destination feature (that is, _auto_ in the Destination menu, or /D by itself in a FuncFit command).
The xw and yw waves are not your data waves. They are created by Igor during the execution of CurveFit, FuncFit or FuncFitMD and filled with data from your input waves. They will be destroyed when fitting is finished. For debugging, you can use Duplicate to save a copy of the waves. Altering the contents of the xw wave will have no effect.

The example above uses xw as an argument to the exp function, and it uses the special features of a wave assignment statement to satisfy point 2.

The next example fits a convolution of a Gaussian peak with an exponential decay. It fits a baseline offset, amplitude and width of the Gaussian peak and the decay constant for the exponential. This might model an instrument with an exponentially decaying impulse response in order to recover the width of an impulsive signal.

Function convfunc(pw, yw, xw) : FitFunc
	WAVE pw, yw, xw

	// pw[0] = gaussian baseline offset
	// pw[1] = gaussian amplitude
	// pw[2] = gaussian position
	// pw[3] = gaussian width
	// pw[4] = exponential decay constant of instrument response

	// Make a wave to contain an exponential with decay
	// constant pw[4]. The wave needs enough points to allow
	// any reasonable decay constant to get really close to zero.
	// The scaling is made symmetric about zero to avoid an X
	// offset from Convolve/A
	Variable dT = deltax(yw)
	Make/D/O/N=201 expwave					// Long enough to allow decay to zero
	SetScale/P x -dT*100,dT,expwave

	// Fill expwave with exponential decay
	expwave = (x>=0)*pw[4]*dT*exp(-pw[4]*x)

	// Normalize exponential so that convolution doesn't change
	// the amplitude of the result
	Variable sumexp
	sumexp = sum(expwave)
	expwave /= sumexp

	// Put a Gaussian peak into the output wave
	yw = pw[1]*exp(-((x-pw[2])/pw[3])^2)

	// Convolve with the exponential. NOTE /A.
	Convolve/A expwave, yw

	// Add the vertical offset AFTER the convolution to avoid end effects
	yw += pw[0]
End

Some things to be aware of with regard to this function:

A wave is created inside the function to store the exponential decay. Making a wave can be a time-consuming operation; it is less convenient for the user of the function, but can save computation time if you make a suitable wave ahead of time and then simply reference it inside the function.
The wave containing the exponential decay ispassed to the convolve operation. The use of the /A flag prevents the convolve operation from changing the length of the output wave yw. You may wish to read the section on Convolution.
The output wave yw is used as a parameter to the convolve operation. Since the convolve operation assumes that the data are evenly-space, this use of yw means that the function does not satisfy points 2) or 3) above. If you use input data to the fit that has missing points or unevenly-spaced X values, this function will fail.

You may also find the section Waveform Arithmetic and Assignment helpful.

Here is a (much) more complicated version of the fitting function that solves these problems, and also is more robust in terms of accuracy. The comments in the code explain how the function works.

Note that this function makes at least two different waves using the Make operation, and that we have used Make/D to make the waves double-precision. This can be crucial. To improve performance and reduce clutter in your Igor experiment file, we create the intermediate waves as free waves.

Function convfunc(pw, yw, xw) : FitFunc
	WAVE pw, yw, xw

	// pw[0] = gaussian baseline offset
	// pw[1] = gaussian amplitude
	// pw[2] = gaussian position
	// pw[3] = gaussian width
	// pw[4] = exponential decay constant of instrument response

	// Make a wave to contain an exponential with decay
	// constant pw[4]. The wave needs enough points to allow
	// any reasonable decay constant to get really close to zero.
	// The scaling is made symmetric about zero to avoid an X
	// offset from Convolve/A.
	
	// resolutionFactor sets the degree to which the exponential
	// will be over-sampled with regard to the problem's parameters.
	// Increasing this number increases the number of time
	// constants included in the calculation. It also decreases
	// the point spacing relative to the problem's time constants.
	// Increasing will also increase the time required to compute

	Variable resolutionFactor = 10
	// dt contains information on important time constants.
	// We wish to set the point spacing for model calculations 
	// much smaller than the exponential time constant or gaussian width.
	// Use absolute values to prevent failures if an iteration strays
	// into unmeaningful but mathematically allowed negative territory.
	
	Variable absDecayConstant = abs(pw[4])
	Variable absGaussWidth = abs(pw[3])
	Variable dT = min(absDecayConstant/resolutionFactor, absGaussWidth/resolutionFactor)

	// Calculate suitable number points for the exponential. Length
	// of exponential wave is 10 time constants; doubled so
	// exponential can start in the middle; +1 to make it odd so
	// exponential starts at t=0, and t=0 is exactly the middle 
	// point. That is better for the convolution.

	Variable nExpWavePnts = round((10*absDecayConstant)/dT)*2 + 1	
	
	// Important: Make double-precision waves.
	// We make free waves to improve performance and so that
	// the intermediate waves clean themselves up at the end of
	// function execution.
				
	Make/D/FREE/O/N=(nExpWavePnts) expwave	// Double-precision free wave

	// In this version of the function, we make a y output wave
	// ourselves, so that we can control the resolution and 
	// accuracy of the calculation. It also will allow us to use
	// a wave assignment later to solve the problem of variable
	// X spacing or missing points.

	Variable nYPnts = max(resolutionFactor*numpnts(yw), nExpWavePnts)
	Make/D/FREE/O/N=(nYPnts) yWave			// Double-precision free wave
	
	// This wave scaling is set such that the exponential will 
	// start at the middle of the wave
	SetScale/P x -dT*(nExpWavePnts/2),dT,expwave			

	// Set the wave scaling of the intermediate output wave to have
	// the resolution calculated above, and to start at the first
	// X value.
	SetScale/P x xw[0],dT, yWave

	// Fill expwave with exponential decay, starting with X=0
	expwave = (x>=0)*dT/pw[4]*exp(-x/pw[4])

	// Normalize exponential so that convolution doesn't change
	// the amplitude of the result
	Variable sumexp
	sumexp = sum(expwave)
	expwave /= sumexp

	// Put a Gaussian peak into the intermediate output wave. We use
	// our own wave (yWave) because the convolution requires a wave
	// with even spacing in X, whereas we may get X values input that
	// are not evenly spaced.
	// Also, we do not add the vertical offset here - it will cause problems
	// with the convolution. Before the convolution Igor zero-pads the
	// wave, so the baseline here must be zero. Otherwise there is
	// a step function at the start of the convolution.
	yWave = pw[1]*exp(-((x-pw[2])/pw[3])^2)

	// Now convolve with the exponential. NOTE /A.
	Convolve/A expwave, yWave
	
	// Move appropriate values corresponding to input X data into 
	// the output Y wave. We use a wave assignment involving the
	// input X wave. This will extract the appropriate values from
	// the intermediate wave, interpolating values where the
	// intermediate wave doesn't have a value precisely at an X
	// value that is required by the input X wave. This wave
	// assignment also solves the problem with auto-destination:
	// The function can be called with an X wave that sets any X
	// spacing, so it doesn't matter what X values are required.
	// This is the appropriate place to add the vertical offset.
	yw = yWave(xw[p]) + pw[0]
End

Note that all the waves created in this function are double-precision. If you don't use the /D flag with the Make operation, Igor makes single-precision waves. Curve fitting computations can be very sensitive to floating-point roundoff errors. We have solved many user problems by simply making intermediate waves double precision.

Note that none of the computations involve the wave yw. That was done so that the computations could be done at finer resolution than the resolution of the data to be fit. By making a separate wave, it is not necessary to modify yw.

The actual return values are picked out of yWave and stored in yw using the special X-scale-based indexing available for one-dimensional waves in a wave assignment. This allows any arbitrary X values in the xw input wave, so long as the intermediate computations are done over the full X range included in xw.

Multivariate All-At-Once Fitting Functions

A multivariate all-at-once fitting function is accepts more than one independent variable. To make one, simply add additional waves after the xw wave:

Function MultivariateAllAtOnce(pw, yw, xw1, xw2) : FitFunc
	WAVE pw, yw, xw1, xw2

	yw = <expression involving pw and all the xw waves>
End

This example accepts two independent variables, xw1 and xw2. If you have more, add additional X wave parameters.

All the X waves are 1D waves with the same number of points as the Y wave, yw, even if your input data is in the form of a matrix wave. If you use FuncFitMD to fit an N row by M column matrix, Igor unrolls the matrix to form a 1D Y wave containing NxM points. This is passed to your function as the Y wave parameter. The X wave parameters are 1D waves containing NxM points with values that repeat for each column.

If you know that the input data fall into a fully-formed matrix wave, you may be able to temporarily re-fold the yw wave into a matrix using the Redimension operation:

Function MultivariateAllAtOnce(pw, yw, xw1, xw2) : FitFunc
	WAVE pw, yw, xw1, xw2

	Redimension/N=(rows, columns) yw
	MatrixOP yw = <matrix math expression>
	Redimension/N=(rows*columns) yw

	yw = <expression involving pw and all the xw waves>
End

Use this technique with great caution, though. In order to know the appropriate rows and columns for the Redimension command, you must make assumptions about the size of the original data set. If there are missing values (NaNs) in the original input matrix, these values will be missing from the Y wave, resulting in fewer points than you would expect.

If you use this technique, you will not be able to use the auto-destination feature (the /D flag with no destination wave) because the auto-destination wave is pretty much guaranteed to be a different size than you expect.

Similarly to the second example all-at-once function above, you can create an intermediate matrix wave and then use wave assignment to get values from the matrix to assign to the yw wave. It may be tricky to figure out how to extract the correct values from your intermediate matrix.

Structure Fit Functions

Sometimes you may need to transmit extra information to a fitting function. This might include constants that need to be set to reflect conditions in a run, but should not be fit; or a wave containing a look-up table or a measured standard sample that is needed for comparison. Perhaps your fit function is very complex and needs some sort of book-keeping data.

If you use a basic fit function or an all-at-once function, such information must be transmitted via global variables and waves. That, in turn, requires that this global information be looked up inside the fit function. The global data requirement makes it difficult to be flexible: the fit function is tied to certain global variables and waves that must be present for the function to work. In addition to adding complexity and difficulty to management of global information, it adds a possible time-consuming operation: looking up the global information requires examining a list of waves or variables, and comparing the names to the desired name.

Structure fit functions are ideal for such problems because they take a single parameter that is a structure of your own design. The first few members of the structure must conform to certain requirements, but the rest is up to you. You can include any kind of data in the structure. An added bonus is that you can include members in the structure that identify for the fit function which fit coefficient is being perturbed when calculating numerical derivatives, that signal when the fit function is being called to fill in the auto-destination wave, and identify when a new fit iteration is starting. You can pass back a flag to tell FuncFit to abandon fitting.

To use a structure fit function, you must do three things:

Define a structure containing certain standard items at the top.
Write a fitting function that uses that structure as its only parameter.
Write a wrapper function for FuncFit that creates an instance of your structure, initializes it and invokes FuncFit with the /STRC parameter flag.

You should familiarize yourself with the use of structures before attempting to write a structure fit function (see Structures In Functions).

Structure fit functions come in basic and all-at-once variants; the difference is determined by the members at the beginning of the structure. The format for the structure for a basic structure fit function is:

Structure myBasicFitStruct
	Wave coefw
	Variable x
	<whatever further elements you like>
EndStructure

The name of the structure can be anything you like that conforms to Igor's naming rules; all that is required is that the first two fields be a wave and a variable. By convention we name the wave coefw and the variable x to match the use of those members. These members of the structure are equivalent to wave and variable parameters required of a basic fit function.

You may wish to use an all-at-once structure fit function for the same reason you might use a regular all-at-once fit function. The same concerns apply to all-at-once structure fit functions; you should read and understand the section All-At-Once Fitting Functions before attempting to write an all-at-once structure fit function.

The structure for an all-at-once structure fit function looks like this:

Structure myAllAtOnceFitStruct
	Wave coefw
	Wave yw
	Wave xw
	<whatever further elements you like>
EndStructure

The first three members of the structure are equivalent to the pw, yw, and xw parameters required in a regular all-at-once fit function.

A simple example of fitting with a structure fit function follows. More examples are available in the File menu: select appropriate examples from Examples→Curve Fitting.

Basic Structure Fit Function Example

As an example of a basic structure fit function, we will write a fit function that fits an exponential decay using an X offset to compensate for numerical problems that can occur when the X range of an exponential function is small compared to the X values. The X offset must not be a fit coefficient because it is not mathematically distinguishable from the decay amplitude. We will write a structure that carries this constant as a custom member of a structure. This function will duplicate the built-in exp_XOffset function (see Built-in Curve Fitting Functions).

First, a fake data set to try it on. Select these commands and type Control-Enter:

Make/D/O/N=100 expData,expDataX
expDataX = enoise(0.5)+100.5
expData = 1.5+2*exp(-(expDataX-100)/0.2) + gnoise(.05)
Display expData vs expDataX
ModifyGraph mode=3,marker=8

Now the code. Copy this code and paste it into your Procedure window:

// The structure definition
Structure expFitStruct
	Wave coefw		// required coefficient wave
	Variable x		// required X value input
	Variable x0	// constant
EndStructure

// the fitting function
Function fitExpUsingStruct(s) : FitFunc
	Struct expFitStruct &s
	
	return s.coefw[0] + s.coefw[1]*exp(-(s.x-s.x0)/s.coefw[2])
End

// The driver function that calls FuncFit:
Function expStructFitDriver(pw, yw, xw, xOff)
	Wave pw	// coefficient wave- pre-load it with initial guess
	Wave yw
	Wave xw
	Variable xOff
	Variable doODR
	
	// an instance of the structure. We initialize the x0 constant only,
	// Igor (FuncFit) will initialize coefw and x as required.
	STRUCT expFitStruct fs
	fs.x0 = xOff	// set the value of the X offset in the structure

	FuncFit fitExpUsingStruct, pw, yw /X=xw /D /STRC=fs

	// no history report for structure fit functions. We print our own
	// simple report here:
	print pw
	Wave W_sigma
	print W_sigma
End

Finally, make a coefficient wave loaded with initial guesses and invoke our driver function:

Make/D/O expStructCoefs = {1.5, 2, .2}
expStructFitDriver(expStructCoefs, expData, expDataX, 100)

This is a very simple example, intended to show only the most basic aspects of fitting with a structure fit function. An advanced programmer could add a control panel user interface, plus code to automatically calculate initial guesses and provide a default value of the x0 constant.

The WMFitInfoStruct Structure

In addition to the required structure members, you can include a WMFitInfoStruct structure member immediately after the required members. The WMFitInfoStruct structure, if present, will be filled in by FuncFit with information about the progress of fitting, and includes a member allowing you to stop fitting if your fit function detects a problem.

Adding a WMFitInfoStruct member to the structure in the example above:

Structure expFitStruct
	Wave coefw	// required coefficient wave
	Variable x	// required X value input
	STRUCT WMFitInfoStruct fi	// optional WMFitInfoStruct
	Variable x0	// constant
EndStructure

And the members of the WMFitInfoStruct:

Member	Description
char IterStarted	Nonzero on the first call of an iteration.
char DoingDestWave	Nonzero when called to evaluate the autodestination wave.
char StopNow	Fit function sets this to nonzero to indicate that a problem has occurred and fitting should stop.
Int32 IterNumber	Number of iterations completed.
Int32 ParamPerturbed	Index of the fit coefficient being perturbed for the calculation of numerical derivatives. Set to -1 when evaluating a solution point with no perturbed coefficients.

The IterStarted and ParamPerturbed members may be useful in some obscure cases to short-cut lengthy computations. The DoingDestWave member may be useful in an all-at-once structure fit function.

Multivariate Structure Fit Functions

To fit multivariate functions (those having more than one dimension or independent variable) you simply use an array for the X member of the structure. For instance, for a basic 2D structure fit function:

Structure My2DFitStruct
	Wave coefw
	Variable x[2]
	<whatever further elements you like>
EndStructure

Or a 2D all-at-once structure fit function:

Structure My2DAllAtOnceFitStruct
	Wave coefw
	Wave yw
	Wave xw[2]
	<whatever further elements you like>
EndStructure

Curve Fitting Using Commands

A few curve fitting features are not completely supported by the Curve Fitting dialog, such as constraints involving combinations of fit coefficients, or user-defined fit functions involving more complex constructions. Also, you might sometimes want to batch-fit to a number of data sets without interacting with the dialog for each data set. These circumstances will require that you use command lines to do fits.

The easiest way to do this is to use the Curve Fitting dialog to generate command lines that do almost what you want. If you simply want to add a more complex feature, such as a more complicated constraint expression, click the To Cmd Line button, then edit the commands generated by the dialog to add the features you want.

If you are writing a user procedure that does curve fitting, you can click the To Clip button to copy the commands generated by the dialog. Then paste the commands into the Procedure window. Edit them as needed by your application.

Curve fitting is done by three operations — CurveFit, FuncFit, and FuncFitMD. You will find details on these operations in the Reference.

Batch Fitting

If you are doing batch fitting, you probably want to call a curve fitting operation inside a loop. In that case, you probably don't want a history report for every fit- it could possible make a very large amount of text in the history. You probably don't want the progress window during the fits- it slows down the fit and will make a flashing window as it appears and disappears. Finally, you probably don't want graphs and tables updating during the fits, as this can slow down computation considerably.

Here is an example function that will do all of this, plus it checks for an error during the fit. If the use of the $ operator is unfamiliar you will want to consult Accessing Waves in Functions.

Function FitExpToListOfWaves(theList)
	String theList
	
	Variable i=0
	string aWaveName = ""
	Variable V_fitOptions = 4	// suppress progress window
	Variable V_FitError = 0	// prevent abort on error
	do
		aWaveName = StringFromList(i, theList)
		WAVE/Z aWave = $aWaveName
		if (!WaveExists(aWave))
			break
		endif
		
		// /N suppresses screen updates during fitting
		// /Q suppresses history output during fitting
		CurveFit/N/Q exp aWave /D/R
		WAVE W_coef

		// save the coefficients
		Duplicate/O W_coef $("cf_"+aWaveName)
		// save errors
		Duplicate/O W_sigma, $("sig_"+aWaveName)
		if (V_FitError != 0)
			// Mark the results as being bad
			WAVE w = $("cf_"+aWaveName)
			w = NaN
			WAVE w = $("sig_"+aWaveName)
			w = NaN
			WAVE w = $("fit_"+aWaveName)
			w = NaN
			WAVE w = $("Res_"+aWaveName)
			w = NaN
			V_FitError = 0
		endif
		i += 1
	while(1)
End

This function is very limited. It simply does fits to a number of waves in a list. Igor includes a package that adds a great deal of sophistication to batch fitting, and provides a user interface. For a demonstration, choose File→Example Experiments→Curve Fitting→Batch Curve Fitting Demo.

Curve Fitting Examples

The Igor Pro Folder includes a number of example experiments that demonstrate the capabilities of curve fitting. These examples cover fitting with constraints, multivariate fitting, multipeak fitting, global fitting, fitting a line between cursors, and fitting to a user-defined function. All of these experiments can be found in Igor Pro Folder/Examples/Curve Fitting.

Singularities in Curve Fitting

You may occasionally run across a situation where you see a "singular matrix" error. This means that the system of equations being solved to perform the fit has no unique solution. This generally happens when the fitted curve contains degeneracies, such as if all Y values are equal.

In a fit to a user-defined function, a singular matrix results if one or more of the coefficients has no effect on the function's return value. Your coefficients wave must have the exact same number of points as the number of coefficients that you actually use in your function or else you must hold constant unused coefficients.

Certain functions may have combinations of coefficients that result in one or more of the coefficients having no effect on the fit. Consider the Gaussian function:

\displaystyle K_{0}+K_{1} \exp \left(\left(x-K_{2}\right) / K_{3}\right)^{2}

If K₁ is set to zero, then the following exponential has no effect on the function value. The fit will report which coefficients have no effect. In this example, it will report that K₂ and K₃ have no effect on the fit. However, as this example shows, it is often not the reported coefficients that are at fault.

Special Considerations for Polynomial Fits

Polynomial fits use the singular value decomposition technique. If you encounter singular values and some of the coefficients of the fit have been zeroed, you are probably asking for more terms than can be supported by your data. You should use the smallest number of terms that gives a "reasonable" fit. If your data does not support higher-order terms then you can actually get a poorer fit by including them.

If you really think your data should fit with the number of terms you specified, you can try adjusting the singular value threshold. You do this by creating a special variable called V_tol and setting it to a value smaller than the default value of 1e-10. You might try 1e-15.

Another way to run into trouble during polynomial fitting is to use a range of X values that are very much offset from zero. The solution is to temporarily offset your X values, do the fit and then restore the original X values. This is done for you by the poly_XOffset fit function; see Built-in Curve Fitting Functions for details.

Errors Due to X Values with Large Offsets

The single and double exponential fits can be thrown off if you try to fit to a range of X values that are very much offset from zero. In general, any function, which, when extrapolated to zero, returns huge or infinite values, can create problems. The solution is to temporarily offset your x values, perform the fit and then restore the original x values. You may need to perform a bit of algebra in order to fix up the coefficients.

As an example consider a fit to an exponential where the x values range from 100 to 101. We temporarily offset the x values by 100, perform the fit and then restore the x values by adding 100. When we did the fit, rather than fitting to k0 + k1 * exp(-k2 * x) we really did the fit to c0 + c1 * exp(-c2 * (x - 100)). A little rearrangement and we have c0 + c1 * exp(-c2 * x) * exp(c2 * 100). Comparing these expressions, we see that k0= c0, k1= c1 * exp(c2 * 100) and k2= c2.

A better solution to the problem of fitting exponentials with large X offsets is to use the built-in exp_XOffset and dblexp_XOffset fit functions. These fit functions automatically incorporate the X shifting; see Built-in Curve Fitting Functions for details.

The same problem can occur when fitting to high-degree polynomials. In this case, the algebra required to transform the solution coefficients back to unoffset X values is nontrivial. It would be better to simply redefine your problem in terms of offset X value.

Curve Fitting Troubleshooting

If you are getting unsatisfactory results from curve fitting you should try the following before giving up.

Make sure your data is valid. It should not be all one value. It should bear some resemblance to the function that you're trying to fit it to.

If the fit is iterative try different initial guesses. Some fit functions require initial guesses that are very close to the correct solution.

If you are fitting to a user-defined function, check the following:

Your coefficients wave must have exactly the same number of points as the number of coefficients that you actually use in your function unless you hold constant the unused coefficients.
Your initial guesses should not be zero unless the expected range is near 1.0 or you have specified an epsilon wave. See The Epsilon Wave for details.
Ensure that your function is working properly. Try plotting it over a representative domain.
Examine your function to ensure all your coefficients are distinguishable. For example in the fragment (k0 + k1) * x, k0 and k1 are indistinguishable. If this situation is detected, the history will contain the message: "Warning: These parameters may be linearly dependent:" followed by a line listing the two parameters that were detected as being indistinguishable.
Because the derivatives for a user-defined fit function are calculated numerically, if the function depends only weakly on a coefficient, the derivatives may appear to be zero. The solution is to create an epsilon wave and set its values large enough to give a nonzero difference in the function output. See The Epsilon Wave for details.
A variation the previous problem is a function that changes in a step-wise fashion, or is "noisy" because an approximation is used that is good to only a limited precision. Again, create an epsilon wave and set the values large enough to give nonzero differences that are of consistent sign.
Verify that each of your coefficients has an effect on the function. In some cases, a coefficient may have an effect over a limited range of X values. If your data do not sample that range adequately the fit may not work well, or may give a singular matrix error.
Make sure that the optimal value of your coefficients is not infinity (it takes a long time to increment to infinity).
Check to see if your function could possibly return NaN or INF for any value of the coefficients. You might be able to add constraints to prevent this from happening. You will see warnings if a singular matrix error resulted from NaN or INF values returned by the fitting function.
Use a double-precision coefficient wave. Curve fitting is numerically demanding and usually works best if all computations are done using double precision numbers. Using a single-precision coefficient wave often causes failures due to numeric truncation. Because the Make operation defaults to single precision, you must use the /D flag when creating your coefficient wave.
If you use intermediate waves in your user-defined fit function, make sure they are all double precision. Because the Make operation defaults to single precision, you must use the /D flag when creating your intermediate waves.

The Epsilon Wave

Curve fitting uses partial derivatives of your fit function with respect to the fit coefficients in order to find the gradient of the chi-square surface. It then solves a linearized estimate of the chi-square surface to find the next estimate of the solution (the minimum in the chi-square surface).

Since Igor doesn't know the mathematical equation for your fit function, it must approximate derivatives numerically using finite differences. That is, a model value is calculated at the present estimate of the fit coefficients, then each coefficient is perturbed by a small amount, and the derivative is calculated from the difference. This small perturbation, which is different for each coefficient, is called "epsilon".

You can specify the epsilon value for each coefficient by providing an epsilon wave to the CurveFit or FuncFit operations using the /E flag. If you do not provide an epsilon wave, Igor determines epsilon for each coefficient using these rules:

If the coefficient wave is single precision (not recommended):

if coef[i] == 0
	eps[i] = 1e-4
else
	eps[i] = 1e-4*coef[i]

If the coefficient wave is double precision:

if coef[i] == 0
	eps[i] = 1e-10
else
	eps[i] = 1e-10*coef[i]

In the Curve Fitting dialog, when you are using a user-defined fitting function, you can select an epsilon wave from the Epsilon Wave menu. When you select _New Wave_, or if you select an existing wave from the menu, Igor adds a column to the Coefficients list where you can edit the epsilon values.

There are a couple of reasons for explicitly setting epsilon. One is if your fit function is insensitive to a coefficient. That is, perturbing the coefficient makes a very small change in the model value. Sometimes the dependence of the model is so small that floating-point truncation results in no change in the model value. You have to set epsilon to a sufficiently large value that the model actually changes when the perturbation is applied.

You also need to set epsilon is when the model is discrete or noisy. This can happen if the model involves a table look-up or a series solution of some sort. In the case of table look-up, epsilon needs to be large enough to make sure that you get two distinct values out of the table.

In the case of a series solution, you have to stop summing terms in the series at some point. If the truncation of the series results in less than full floating-point resolution of the series, you need to make sure epsilon is large enough that the change in the model is larger than the resolution of the series. A series might include something like a numerical solution of an ODE, using the IntegrateODE operation. It could also involve FindRoots or Optimize, each of which gives you an approximate result. Since these operations run faster if you don't demand high precision, there may be a strong incentive to decrease the accuracy of the computation, and that may in turn lead to a need for an epsilon wave.

Curve Fitting References

An explanation of the Levenberg-Marquardt nonlinear least squares optimization can be found in Chapter 14.4 of:

Press, W.H., B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling, Numerical Recipes in C, Cambridge University Press, 1988.

The algorithm used for applying constraints is given in:

Shrager, Richard, Quadratic Programming for Nonlinear Regression, Communications of the ACM, v. 15, pp. 41-45, 1972.

The method is described in gory mathematical detail in:

Shrager, Richard, Nonlinear Regression With Linear Constraints: An Extension of the Magnified Diagonal Method, Journal of the Association for Computing Machinery, 17, 446-452, 1970.

References for the ODRPACK95 package used for orthogonal distance regression:

Boggs, P.T., R.H. Byrd, and R.B. Schnabel, A Stable and Efficient Algorithm for Nonlinear Orthogonal Distance Regression, SIAM Journal of Scientific and Statistical Computing, 8, 1052-1078, 1987.

Boggs, P.T., R.H. Byrd, J.R. Donaldson, and R.B. Schnabel, Algorithm 676 - ODRPACK: Software for Weighted Orthogonal Distance Regression, ACM Transactions on Mathematical Software, 15, 348-364, 1989

Boggs, P.T., J.R. Donaldson, R.B. Schnabel and C.H. Spiegelman, A Computational Examination of Orthogonal Distance Regression, Journal of Econometrics, 38, 169-201, 1988.

An exhaustive, but difficult to read source for nonlinear curve fitting:

Seber, G.A.F, and C.J. Wild, Nonlinear Regression, John Wiley & Sons, 1989.

A discussion of the assumptions and approximations involved in calculating confidence bands for nonlinear functions is provided in the beginning sections of Chapter 5.

General books on curve fitting and statistics:

Draper, N., and H. Smith, Applied Regression Analysis, John Wiley & Sons, 1966.

Box, G.E.P., W.G. Hunter, and J.S. Hunter, Statistics for Experimenters, John Wiley & Sons, 1978.

Curve Fitting Demos

Open Constraint Demo

Open Global Fit Demo

Open Multi-Peak Fit Demo

Open Multi-Variate Fit Demo

Open Multiple Fits In Threads Demo

Curve Fitting Terminology​

Overview of Curve Fitting​

Iterative Fitting​

Initial Guesses​

Termination Criteria​

Errors in Curve Fitting​

Data for Curve Fitting​

Curve Fitting Using the Quick Fit Menu​

Limitations of the Quick Fit Menu​

Curve Fitting Using the Curve Fitting Dialog​

A Simple Case -- Fitting to a Built-in Function: Line Fit​

Choosing the Function and Data​

Two Useful Additions: Holding a Coefficient and Generating Residuals​

The Automatic Guesses Didn't Work​

Fits with Constants​

Fitting to a User-Defined Function​

The Coefficients Tab for a User-Defined Function​

Fitting to an External Function (XFUNC)​

The Coefficient Wave​

Errors​

The Destination Wave​

No Destination​

Auto-trace​

Explicit Destination​

New Wave​

Fitting a Subset of the Data​

Using a Mask Wave​

Weighting​

Proportional Weighting​

Fitting to a Multivariate Function​

Fitting a Subrange of the Data for a Multivariate Function​

Model Results for Multivariate Fitting​

Multivariate Fitting Examples​

Problems with the Curve Fitting Dialog​

Built-in Curve Fitting Functions​

Inputs and Outputs for Built-in Fits​

Curve Fitting Dialog Tabs​

Global Controls​

Function and Data Tab​

Data Options Tab​

Coefficients Tab​

Output Options Tab​

Computing Residuals​

Residuals Using Auto Trace​

Removing the Residual Auto Trace​

Residuals Using Auto Wave​

Residuals Using an Explicit Residual Wave​

Explicit Residual Wave Using New Wave​

Calculating Residuals After the Fit​

Coefficient of Determination or R-Squared​

R-Squared and Fits Through the Origin​

Estimates of Error​

Confidence Bands and Coefficient Confidence Intervals​

Calculating Confidence Intervals After the Fit​

Confidence Band Waves​

Some Statistics​

Confidence Bands and Nonlinear Functions​

Covariance Matrix​

Correlation Matrix​

Identifiability Problems​

Fitting with Constraints​

Constraints Using the Curve Fitting Dialog​

Complex Constraints Using a Constraints Wave​

Constraint Expressions​

Equality Constraint​

Example Fit with Constraints​

Constraint Matrix and Vector​

Constrained Curve Fitting Pitfalls​

Constraints Demo​

NaNs and INFs in Curve Fits​

Special Variables for Curve Fitting​

V_FitOptions​

Bit 0: Controls X Scaling of Auto-trace Wave​

Bit 1: Robust Fitting​

Bit 2: Suppresses the Curve Fit Window​

Bit 3: Save Iterates​

Bit 4: Suppress Screen Updates​

Bit 5: Errors Only​

V_chisq​

V_q​

Curve Fitting Terminology

Overview of Curve Fitting

Iterative Fitting

Initial Guesses

Termination Criteria

Errors in Curve Fitting

Data for Curve Fitting

Curve Fitting Using the Quick Fit Menu

Limitations of the Quick Fit Menu

Curve Fitting Using the Curve Fitting Dialog

A Simple Case -- Fitting to a Built-in Function: Line Fit

Choosing the Function and Data

Two Useful Additions: Holding a Coefficient and Generating Residuals

The Automatic Guesses Didn't Work

Fits with Constants

Fitting to a User-Defined Function

The Coefficients Tab for a User-Defined Function

Fitting to an External Function (XFUNC)

The Coefficient Wave

Errors

The Destination Wave

No Destination

Auto-trace

Explicit Destination

New Wave

Fitting a Subset of the Data

Using a Mask Wave

Weighting

Proportional Weighting

Fitting to a Multivariate Function

Fitting a Subrange of the Data for a Multivariate Function

Model Results for Multivariate Fitting

Multivariate Fitting Examples

Problems with the Curve Fitting Dialog

Built-in Curve Fitting Functions

Inputs and Outputs for Built-in Fits

Curve Fitting Dialog Tabs

Global Controls

Function and Data Tab

Data Options Tab

Coefficients Tab

Output Options Tab

Computing Residuals

Residuals Using Auto Trace

Removing the Residual Auto Trace

Residuals Using Auto Wave

Residuals Using an Explicit Residual Wave

Explicit Residual Wave Using New Wave

Calculating Residuals After the Fit

Coefficient of Determination or R-Squared

R-Squared and Fits Through the Origin

Estimates of Error

Confidence Bands and Coefficient Confidence Intervals

Calculating Confidence Intervals After the Fit

Confidence Band Waves

Some Statistics

Confidence Bands and Nonlinear Functions

Covariance Matrix

Correlation Matrix

Identifiability Problems

Fitting with Constraints

Constraints Using the Curve Fitting Dialog

Complex Constraints Using a Constraints Wave

Constraint Expressions

Equality Constraint

Example Fit with Constraints

Constraint Matrix and Vector

Constrained Curve Fitting Pitfalls

Constraints Demo

NaNs and INFs in Curve Fits

Special Variables for Curve Fitting

V_FitOptions

Bit 0: Controls X Scaling of Auto-trace Wave

Bit 1: Robust Fitting

Bit 2: Suppresses the Curve Fit Window

Bit 3: Save Iterates

Bit 4: Suppress Screen Updates

Bit 5: Errors Only

V_chisq

V_q